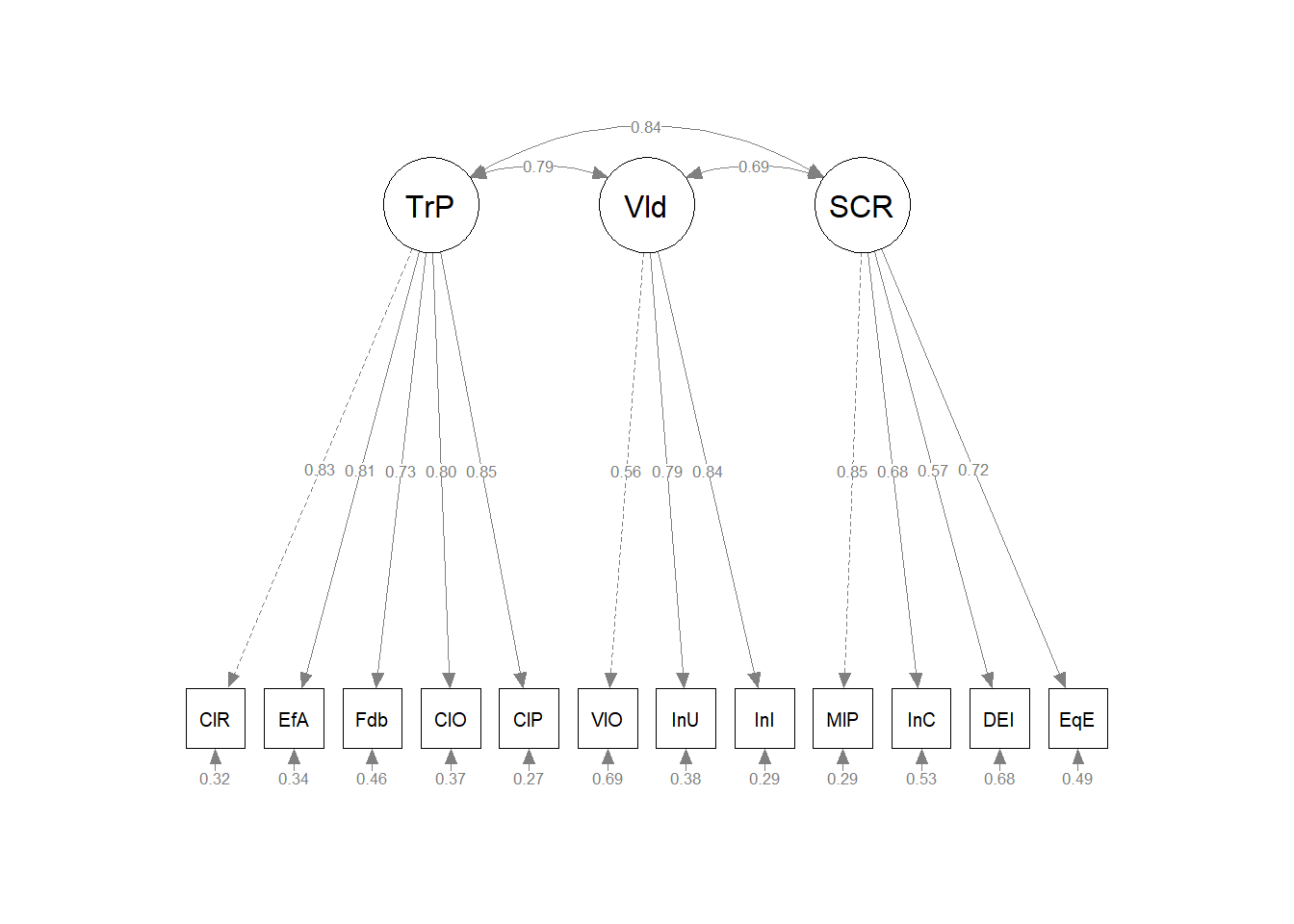
Chapter 11 CFA: Hierarchical and Nested Models
This is the second lecture in our series on confirmatory factor analysis (CFA). In this lesson we will compare first-order structures (with correlated uncorrelated factors) to second-order and bifactor structures. Modification indices will allow us to tweak each model’s fit. We will also determine and track the identification status of models, including nested/nesting models and examining issues of equivalent models.
11.2 CFA Workflow
Below is a screenshot of a CFA workflow. The original document is in the GitHub site that hosts the ReCentering Psych Stats: Psychometrics OER.
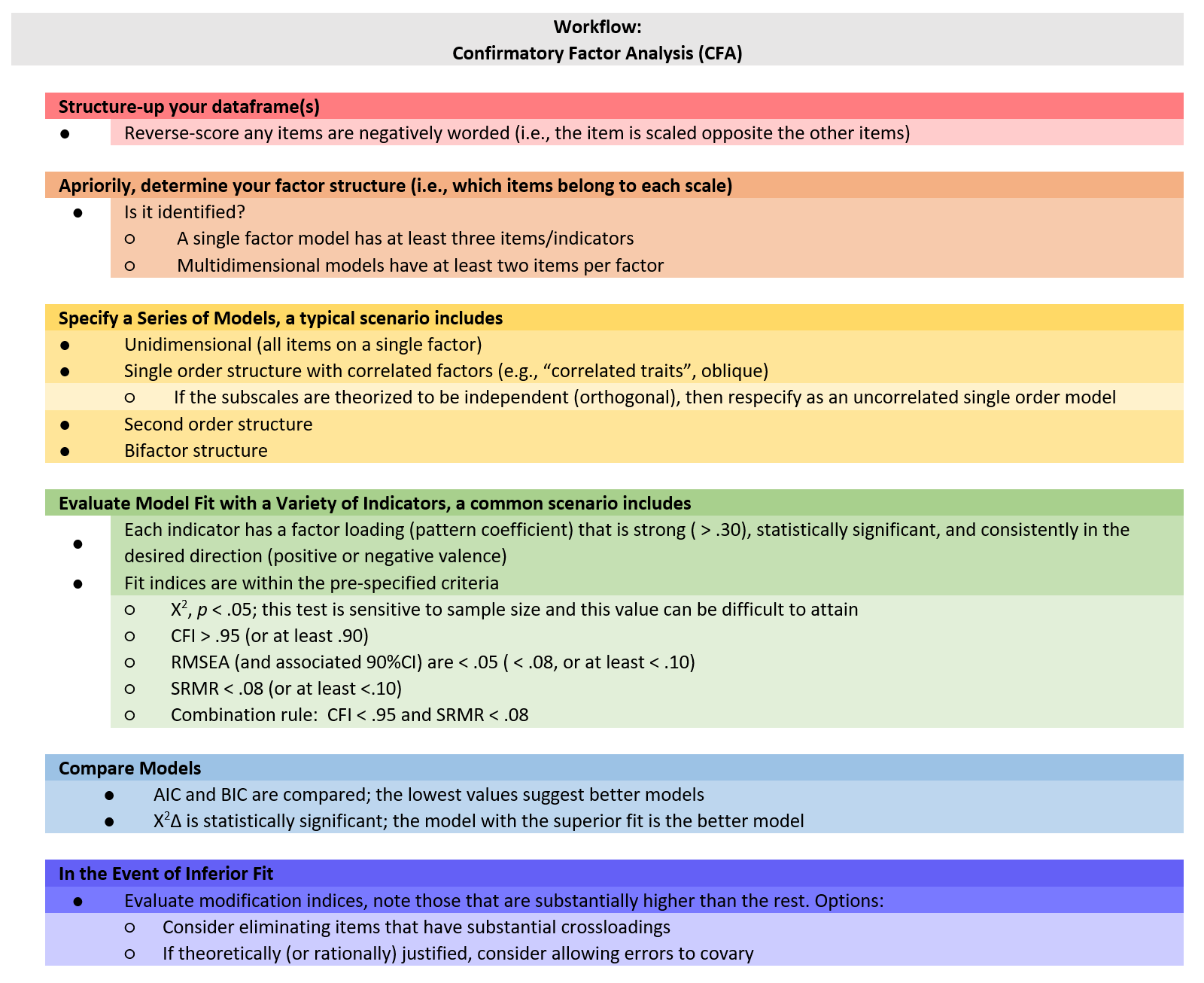
Because the intended audience for the ReCentering Psych Stats OER is the scientist-practitioner-advocate, this lesson focuses on the typical workflow and associated decisions. As you might guess, the details of CFA can be quite complex and require more investigation and decision-making in models that pose more complexity or empirical challenges. The following are the general steps in a CFA.
- Creating an items only dataframe where any items are scaled in the same direction (e.g., negatively worded items are reverse-scored).
- Determining a factor structure that is identified, that is
- a single factor (unidimensional) model has at least three items/indicators
- a multidimensional model with at least two items per factor
- Specify a series of models, these typically include
- a unidimensional model (all items on a single factor)
- a single order structure with correlated factors
- a second order structure
- a bifactor structure
- Evaluate model fit with a variety of indicators
- factor loadings
- fit indices
- Compare models
- In the event of poor model fit, investigate modification indices and consider respecification
- eliminating items
- changing factor membership
- allowing errors to covary
11.3 Another Look at Varying Factor Structures
In this lecture we move into second-order and bifactor models, let’s look again factor structures, considering unidimensional, first-order, and second-order variations.
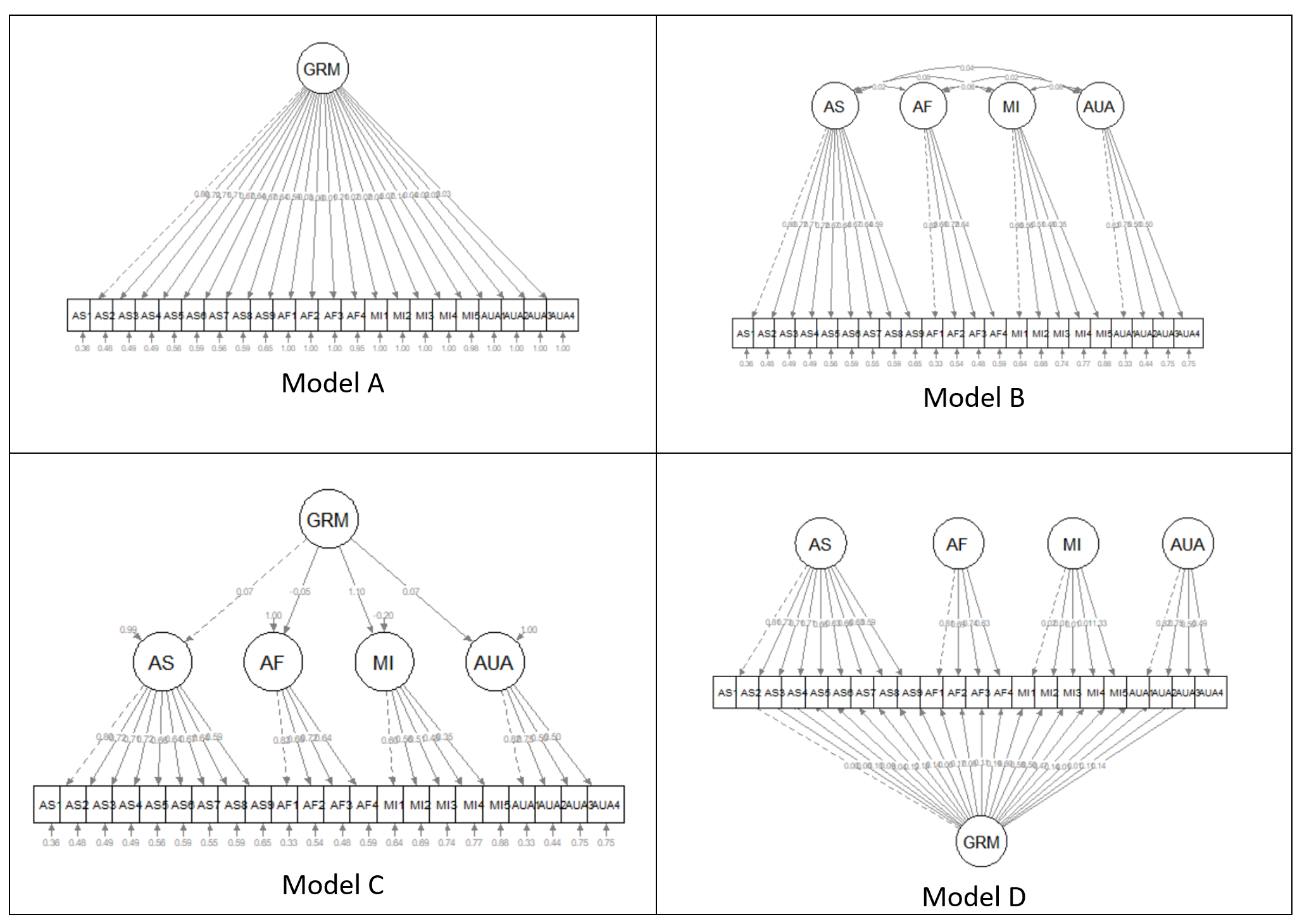
Models A and B are first-order models. Note that all factors are on a single plane.
Model A is unidimensional. Each item is influenced by a single common factor, and defined by a single term that includes systematic and random error. Note that there is only one systematic source of variance for each item AND it is from a single source: F1.
Model B is often referred to as a “correlated traits” model. Here, the larger construct is separated into distinct-yet-correlated elements. The variance of each item is assumed to be a weighted linear function of two or more common factors.
Model C is a second-order factor structure. Rather than merely being correlated, factors are related because they share a common cause. In this model, the second-order factor explains why three or more traits are correlated. Note that there is no direct relationship between the item and the target construct. Rather, the relationship between the second-order factor and each item is mediated through the primary factor (yes, an indirect effect!).
Model D is a bifactor structure. Here, each item loads on a general factor. This general factor (bottom row) reflects what is common among the items and represents the individual differences on the target dimension that a researcher is most interested in. Group factors (top row) are now specified as orthogonal. The group factors represent common factors measured by the items that explain item response variation not accounted for by the general factor. In some research scenarios, the group factors are termed “nuisance” dimensions. That is, that which they have in common interferes with measuring the primary target of interest.
11.4 Revisiting Model Identification
Model identification means it is theoretically possible for a statistical analysis to derive a unique estimate of every model parameter.
Theoretical is emphasizes that identification is a property of the model and not the data; that is, it doesn’t matter if the sample size is 100 or 10,000.
CFA has the same general requirements for identification as other forms of SEM:
- Every latent variable (including errors) must be scaled; and
- Model degrees of freedom must be at least zero \((df_{M}\leq 0)\) (aka “the counting rule”; this means that there must be at least as many observations as there are free parameters)
11.4.1 Identification Status
Underidentified (or underdetermined) models violate the counting rule because there are more free parameters than observations.
For example, solve this equation:
\(a + b = 6\).
There are an infinite number of solutions: 4 + 2, 3 + 3, 2.5 + 3.5…and so on to \(\infty\). When the computing algorithm tries to solve this problem, it will fail to converge.
The parallel scenario in an SEM/CFA model with more free parameters than observations would have negative df.
Just-identified (or just-determined) models have a single unique solution,
\((df_{M} = 0)\)
For example, for this set of equations:
\(a + b = 6\)
\(2a + b = 10\)
The only answer is: \(a = 4, b = 2\)
Overidentified (or overdetermined) models have more observations than free parameters. That is:
\(df_{M} > 0\)
For example, solve for this set of equations:
\(a + b = 6\)
\(2a + b = 10\)
\(3a + b = 12\)
There is no single solution that satisfies all three formulas, but there is a way to find a unique solution. We can impose a statistical criterion that leads to the overidentified/overdetermined circumstance with more observations than free parameters. For example, we could impose the least squares criterion (from regression, but with no intercept/constant in the prediction equation). The constraint (instruction) would read:
Find values of a and b that yield total scores such that the sum of squared differences between the observations (6, 10, 12) and these total scores is as small as possible (and also unique).
In this case, answers are \(a = 3.00, b = 3.33\) and the solutions are 6.44, 9.33, 12.33. While the solution doesn’t perfectly reproduce the data, it facilitates model testing.
The bad news is that SEM/CFA computer tools are generally not helpful in determining whether a model is identified or not. Why? Computers are great a numerical processing, but not symbolic processing (needed for determining identification status). This means that we, the researchers, must learn the identification heuristics to determine the model’s degree of identification.
Need a break already? My favorite scene during The Imitation Game parallels issues of identification, iterations, and convergence. The Turing machine runs and runs until its users can feed it proper start values so that it finally converges on a solution.
Kenny (Kenny, 2012) provides some helpful guidelines in determining model identification with the calculation of knowns and unknowns. In in a standard CFA/SEM specification, knowns are the number of covariances between all the variables in the model, \((k(k+1))/2\), where \(k\) is the number of variables in the model. Unknowns are the free parameters that must be calculated. These include paths; covariances between exogenous variables, between disturbances (error terms), and between exogenous variables and disturbances (error terms); variances of the exogenous variables; and disturbances (error terms) of the endogenous variables (minus the number of linear constraints).
* If $knowns \lt unknowns$ then the model is *under-identified*
* If $knowns = unknowns$ then the model is *just-identified*
* If $knowns \gt unknowns$ then the model is *overidentified*11.4.2 Identification in Practice
It is essential that every latent variable (including errors) must be scaled such that the degrees of freedom for the model be greater than or equal to zero (\(df_{M} \geq 0\)).
Operationally, in a standard CFA model:
- A single factor model needs at least 3 indicators for the single factor.
- Factor models with more than one factor require at least two or more indicators per factor.
- For purposes of identification, more is better with 3-5 being recommended.
(Among other things) nonstandard models occur when:
- errors are allowed to correlate/covary
- complex indicators are defined by more than one factor
We will return to these as we encounter them later in today’s lecture. Essentially, we will need to “subtract” 1 df for every parameter we “free” to covary. This is because we then need to estimate it and it becomes “unknown.”
Empirical underidentification is also a threat. This means, the model fails to converge because of the characteristics of the data. For example, perhaps we specified model on the cusp of identification: 2 factors, correlated, with 2 indicators each. If in fact, the data did not support the correlation between the two factors…because of the “just barely” identified circumstance, you may receive an “empirically underidentified” solution.
Today we are going to specify second-order and bifactor models. As we do each, we will address these issues of model identification.
11.5 Research Vignette
This lesson’s research vignette emerges from Keum et al’s Gendered Racial Microaggressions Scale for Asian American Women (GRMSAAW; (Keum et al., 2018)). The article reports on two separate studies that comprised the development, refinement, and psychometric evaluation of two, parallel, versions (stress appraisal, frequency) of scale. I simulated data from the final construction of the frequency version as the basis of the lecture. If the scale looks somewhat familiar it is because the authors used the Gendered Racial Microaggressions Scale for Black Women (J. A. Lewis & Neville, 2015) as a model.
Keum et al. (2018) reported support for a total scale score (22 items) and four subscales. Below, I list the four subscales, their number of items, and a single example item. At the outset, let me provide a content advisory For those who hold this particular identity (or related identities) the content in the items may be upsetting. In other lessons, I often provide a variable name that gives an indication of the primary content of the item. In the case of the GRMSAAW, I will simply provide an abbreviation of the subscale name and its respective item number. This will allow us to easily inspect the alignment of the item with its intended factor, and hopefully minimize discomfort. If you are not a member of this particular identity, I encourage you to learn about these microaggressions by reading the article in its entirety. Please do not ask members of this group to explain why these microaggressions are harmful or ask if they have encountered them.
There are 22 items on the GRMSAAW scale. Using the same item stems, the authors created two scales. One assesses frequency of the event, the second assesses the degree of stressfulness. I simulated data from the stressfulness scale. Its Likert style scaling included: 0 (not at all stressful), 1(slightly stressful), 2(somewhat stressful), 3(moderately stressful), 4(very stressful), and 5(extremely stressful).
The four factors, number of items, and sample item are as follows:
- Ascribed Submissiveness (9 items)
- Others expect me to be submissive. (AS1)
- Others have been surprised when I disagree with them. (AS2)
- Others take my silence as a sign of compliance. (AS3)
- Others have been surprised when I do things independent of my family. (AS4)
- Others have implied that AAW seem content for being a subordinate. (AS5)
- Others treat me as if I will always comply with their requests. (AS6)
- Others expect me to sacrifice my own needs to take care of others (e.g., family, partner) because I am an AAW. (AS7)
- Others have hinted that AAW are not assertive enough to be leaders. (AS8)
- Others have hinted that AAW seem to have no desire for leadership. (AS9)
- Asian Fetishism (4 items)
- Others express sexual interest in me because of my Asian appearance. (AF1)
- Others take sexual interest in AAW to fulfill their fantasy. (AF2)
- Others take romantic interest in AAW just because they never had sex with an AAW before. (AF3)
- Others have treated me as if I am always open to sexual advances. (AF4)
- Media Invalidation (5 items)
- I see non-Asian women being casted to play female Asian characters.(MI1)
- I rarely see AAW playing the lead role in the media. (MI2)
- I rarely see AAW in the media. (MI3)
- I see AAW playing the same type of characters (e.g., Kung Fu woman, sidekick, mistress, tiger mom) in the media. (MI4)
- I see AAW characters being portrayed as emotionally distant (e.g., cold-hearted, lack of empathy) in the media. (MI5)
- Assumptions of Universal Appearance (4 items)
- Others have talked about AAW as if they all have the same facial features (e.g., eye shape, skin tone). (AUA1)
- Others have suggested that all AAW look alike.(AUA2)
- Others have talked about AAW as if they all have the same body type (e.g., petite, tiny, small-chested). (AUA3)
- Others have pointed out physical traits in AAW that do not look ‘Asian’.
Four additional scales were reported in the Keum et al. article (Keum et al., 2018). Fortunately, I was able to find factor loadings from the original psychometric article or subsequent publications. For multidimensional scales, I assign variable names according to the scale to which the item belongs (e.g., Env42). In contrast, when subscales or short unidimensional scales were used, I assigned variable names based on item content (e.g., “blue”). In my own work, I prefer item-level names so that I can quickly see (without having to look up the item names) how the items are behaving. The scales, their original citation, and information about how I simulated data for each are listed below.
- Racial Microaggressions Scale (RMAS; (Torres-Harding et al., 2012)) is a 32-item scale with Likert scaling ranging from 0 (never) to 3 (often/frequent). Higher scores represent greater frequency of perceived microaggressions. I simulated data at the subscale level. The RMAS has six subscales, but only four (Invisibility, Low-Achieving/Undesirable Culture, Foreigner/Not Belonging,and Environmental Invalidation) were used in the study. Data were simulated using factor loadings (from the four factors) in the source article.
- Schedule of Sexist Events (SSE; (Klonoff & Landrine, 1995)) is a 20-item scale that with Likert scaling ranging from 1 (the event has never happened to me) to 6 (the event happened almost all [i.e., more than 70%] of the time). Higher scores represent greater frequency of everyday sexist events. I simulated data the subscale level. Within two larger scales (recent events, lifetime events), there are three subscales: Sexist Degradation and Its Consequences, Unfair/Sexist Events at Work/School, and Unfair Treatment in Distant and Close Relationships. Data were simulated using factor loadings from the source article.
- PHQ-9 (Kroenke et al., 2001) is a 9-item scale with Likert scaling ranging from 0 (not at all) to 3 (nearly every day). Higher scores indicate higher levels of depression. I simulated data by estimating factor loadings from Brattmyr et al. (2022).
- Internalized Racism in Asian American Scale (IRAAS (Choi et al., 2017)) is a 14-item scale with Likert scaling ranging from 1 (strongly disagree) to 6 (strongly agree). Higher scores indicate greater internalized racism. Data were simulated using the factor loadings from the bifactor model in the source article.
As you consider homework options, there is sufficient simulated data to use the RMAS, SSE, or IRAAS.
Below, I walk through the data simulation. This is not an essential portion of the lesson, but I will lecture it in case you are interested. None of the items are negatively worded (relative to the other items), so there is no need to reverse-score any items.
Simulating the data involved using factor loadings, means, standard deviations, and correlations between the scales. Because the simulation will produce “out-of-bounds” values, the code below rescales the scores into the range of the Likert-type scaling and rounds them to whole values.
#Entering the intercorrelations, means, and standard deviations from the journal article
Keum_GRMS_generating_model <- '
#measurement model
General =~ .50*AS1 + .44*AS2 + .50*AS3 + .33*AS4 + .58*AS5 + .49*AS6 + .51*AS7 + .53*AS8 + .50*AS9 + .53*AF1 + .74*AF2 + .54*AF3 + .52*AF4 + .64*AUA1 + .59*AUA2 + .67*AUA3 + .64*AUA4 + .59*MI1 + .50*MI2 + .52*MI3 + .40*MI4 + .55*MI5
AS =~ .68*AS1 + .65*AS2 + .53*AS3 + .55*AS4 + .54*AS5 + .55*AS6 + .42*AS7 + .47*AS8 + .50*AS9
AF =~ .63*AF1 + .45*AF2 + .56*AF3 + .54*AF4
AUA =~ .55*AUA1 + .55*AUA2 + .31*AUA3 + .31*AUA4
MI =~ .27*MI1 + .53*MI2 + .57*MI3 + .29*MI4 + .09*MI5
RMAS_FOR =~ .66*FOR1 + .90*FOR2 + .63*FOR4
RMAS_LOW =~ .64*LOW22 + .54*LOW23 + .49*LOW28 + .63*LOW29 + .58*LOW30 + .67*LOW32 + .67*LOW35 + .76*LOW36 + .72*LOW37
RMAS_INV =~ .66*INV33 + .70*INV39 + .79*INV40 + .71*INV41 + .71*INV47 + .61*INV49 + .65*INV51 + .70*INV52
RMAS_ENV =~ .71*ENV42 + .70*ENV43 + .74*ENV44 + .57*ENV45 + .54*ENV46
SSEL_Deg =~ .77*LDeg18 + .73*LDeg19 + .71*LDeg21 + .71*LDeg15 + .67*LDeg16 + .67*LDeg13 + .62*LDeg14 + .58*LDeg20
SSEL_dRel =~ .69*LdRel4 + .68*LdRel6 + .64*LdRel7 + .64*LdRel5 + .63*LdRel1 + .49*LdRel3
SSEL_cRel =~ .73*LcRel11 + .68*LcRel9 + .66*LcRel23
SSEL_Work =~ .73*LWork17 + .10*LWork10 + .64*LWork2
SSER_Deg =~ .72*RDeg15 + .71*RDeg21 + .69*RDeg18 + .68*RDeg16 + .68*RDeg13 + .65*RDeg19 + .58*RDeg14 + .47*RDeg20
SSER_dRel =~ .74*RDeg4 + .67*RDeg6 + .64*RDeg5 + .54*RDeg7 + .51*RDeg1
SSER_cRel =~ .69*RcRel9 + .59*RcRel11 + .53*RcRel23
SSER_Work =~ .72*RWork10 + .67*RWork2 + .62*RWork17 + .51*RWork3
SSE_Lifetime =~ SSEL_Deg + SSEL_dRel + SSEL_cRel + SSEL_Work
SSE_Recent =~ SSER_Deg + SSER_dRel + SSEL_cRel + SSER_Work
PHQ9 =~ .798*anhedonia + .425*down + .591*sleep + .913*lo_energy + .441*appetite + .519*selfworth + .755*concentration + .454*too_slowfast + .695*s_ideation
gIRAAS =~ .51*SN1 + .69*SN2 + .63*SN3 + .65*SN4 + .67*WS5 + .60*WS6 + .74*WS7 + .44*WS8 + .51*WS9 + .79*WS10 + .65*AB11 + .63*AB12 + .68*AB13 + .46*AB14
SelfNegativity =~ .60*SN1 + .50*SN2 + .63*SN3 + .43*SN4
WeakStereotypes =~ .38*WS5 + .22*WS6 + .10*WS7 + .77*WS8 + .34*WS9 + .14*WS10
AppearanceBias =~ .38*AB11 + .28*AB12 + .50*AB13 + .18*AB14
#Means
#Keum et al reported total scale scores, I divided those totals by the number of items per scale for mean scores
AS ~ 3.25*1
AF ~ 3.34*1
AUA ~ 4.52
MI ~ 5.77*1
General ~ 3.81*1
RMAS_FOR ~ 3.05*1
RMAS_LOW ~ 2.6*1
RMAS_INV ~ 2.105*1
RMAS_ENV ~ 3.126*1
SSEL_Deg ~ 2.55*1
SSEL_dRel ~ 1.96*1
SSEL_cRel ~ 3.10*1
SSEL_Work ~ 1.66*1
SSER_Deg ~ 2.02*1
SSER_dRel ~ 1.592*1
SSER_cRel ~ 1.777*1
SSER_Work ~ 1.3925*1
SSER_Lifetime ~ 2.8245*1
SSER_Recent ~ 2.4875*1
PHQ9 ~ 1.836*1
gIRAAS ~ 2.246*1
#Correlations
AS ~~ .00*AF
AS ~~ .00*AUA
AS ~~ .00*MI
AS ~~ .00*General
AS ~~ .28*RMAS_FOR
AS ~~ .24*RMAS_LOW
AS ~~ .46*RMAS_INV
AS ~~ .16*RMAS_ENV
AS ~~ .40*SSE_Lifetime
AS ~~ .28*SSE_Recent
AS ~~ .15*PHQ9
AS ~~ .13*gIRAAS
AF ~~ .00*AUA
AF ~~ .00*MI
AF ~~ .00*General
AF ~~ .02*RMAS_FOR
AF ~~ .05*RMAS_LOW
AF ~~ .11*RMAS_INV
AF ~~ .07*RMAS_ENV
AF ~~ .34*SSE_Lifetime
AF ~~ .27*SSE_Recent
AF ~~ -.04*PHQ9
AF ~~ .21*gIRAAS
AUA ~~ .00*MI
AUA ~~ .00*General
AUA ~~ .18*RMAS_FOR
AUA ~~ .20*RMAS_LOW
AUA ~~ .01*RMAS_INV
AUA ~~ -.04*RMAS_ENV
AUA ~~ .02*SSE_Lifetime
AUA ~~ .92*SSE_Recent
AUA ~~ .02*PHQ9
AUA ~~ .17*gIRAAS
MI ~~ .00*General
MI ~~ -.02*RMAS_FOR
MI ~~ .08*RMAS_LOW
MI ~~ .31*RMAS_INV
MI ~~ .36*RMAS_ENV
MI ~~ .15*SSE_Lifetime
MI ~~ .08*SSE_Recent
MI ~~ -.05*PHQ9
MI ~~ -.03*gIRAAS
General ~~ .34*RMAS_FOR
General ~~ .63*RMAS_LOW
General ~~ .44*RMAS_INV
General ~~ .45*RMAS_ENV
General ~~ .54*SSE_Lifetime
General ~~ .46*SSE_Recent
General ~~ .31*PHQ9
General ~~ -.06*gIRAAS
RMAS_FOR ~~ .57*RMAS_LOW
RMAS_FOR ~~ .56*RMAS_INV
RMAS_FOR ~~ .37*RMAS_ENV
RMAS_FOR ~~ .33*SSE_Lifetime
RMAS_FOR ~~ .25*SSE_Recent
RMAS_FOR ~~ .10*PHQ9
RMAS_FOR ~~ .02*gIRAAS
RMAS_LOW ~~ .69*RMAS_INV
RMAS_LOW ~~ .48*RMAS_ENV
RMAS_LOW ~~ .67*SSE_Lifetime
RMAS_LOW ~~ .57*SSE_Recent
RMAS_LOW ~~ .30*PHQ9
RMAS_LOW ~~ .16*gIRAAS
RMAS_INV ~~ .59*RMAS_ENV
RMAS_INV ~~ .63*SSE_Lifetime
RMAS_INV ~~ .52*SSE_Recent
RMAS_INV ~~ .32*PHQ9
RMAS_INV ~~ .23*gIRAAS
RMAS_ENV ~~ .46*SSE_Lifetime
RMAS_ENV ~~ .31*SSE_Recent
RMAS_ENV ~~ .11*PHQ9
RMAS_ENV ~~ .07*gIRAAS
SSE_Lifetime ~~ .83*SSE_Recent
SSE_Lifetime ~~ .30*PHQ9
SSE_Lifetime ~~ .14*gIRAAS
SSE_Recent ~~ .30*PHQ9
SSE_Recent ~~ .20*gIRAAS
PHQ9 ~~ .18*gIRAAS
#Correlations between SES scales from the Klonoff and Landrine article
#Note that in the article the factor orders were reversed
SSEL_Deg ~~ .64*SSEL_dRel
SSEL_Deg ~~ .61*SSEL_cRel
SSEL_Deg ~~ .50*SSEL_Work
SSEL_dRel ~~ .57*SSEL_cRel
SSEL_dRel ~~ .57*SSEL_Work
SSEL_cRel ~~ .47*SSEL_Work
SSER_Deg ~ .54*SSER_dRel
SSER_Deg ~ .54*SSER_Work
SSER_Deg ~ .59*SSER_cRel
SSER_dRel ~ .56*SSER_Work
SSER_dRel ~ .46*SSER_cRel
SSER_Work ~ .43*SSER_cRel
SSE_Lifetime ~ .75*SSE_Recent
'
set.seed(240311)
dfGRMSAAW <- lavaan::simulateData(model = Keum_GRMS_generating_model,
model.type = "sem",
meanstructure = T,
sample.nobs=304,
standardized=FALSE)
#used to retrieve column indices used in the rescaling script below
col_index <- as.data.frame(colnames(dfGRMSAAW))
#The code below loops through each column of the dataframe and assigns the scaling accordingly
#Rows 1 thru 22 are the GRMS items
#Rows 23 thru 47 are the RMAS
#Rows 48 thru 87 are the SSE
#Rows 88 thru 96 are the PHQ9
#Rows 97 thru 110 are the IRAAS
#Rows 111 thru 112 are scale scores for SSE
for(i in 1:ncol(dfGRMSAAW)){
if(i >= 1 & i <= 22){
dfGRMSAAW[,i] <- scales::rescale(dfGRMSAAW[,i], c(0, 5))
}
if(i >= 23 & i <= 47){
dfGRMSAAW[,i] <- scales::rescale(dfGRMSAAW[,i], c(0, 3))
}
if(i >= 48 & i <= 87){
dfGRMSAAW[,i] <- scales::rescale(dfGRMSAAW[,i], c(1, 6))
}
if(i >= 88 & i <= 96){
dfGRMSAAW[,i] <- scales::rescale(dfGRMSAAW[,i], c(0, 3))
}
if(i >= 97 & i <= 110){
dfGRMSAAW[,i] <- scales::rescale(dfGRMSAAW[,i], c(1, 6))
}
}
#rounding to integers so that the data resembles that which was collected
library(tidyverse)
dfGRMSAAW <- dfGRMSAAW %>% round(0)
#quick check of my work
#psych::describe(dfGRMSAAW) The optional script below will let you save the simulated data to your computing environment as either an .rds object or a .csv file.
An .rds file preserves all formatting to variables prior to the export and re-import. For the purpose of this chapter, you don’t need to do either. That is, you can re-simulate the data each time you work the problem.
# to save the df as an .rds (think 'R object') file on your computer;
# it should save in the same file as the .rmd file you are working
# with saveRDS(dfGRMSAAW, 'dfGRMSAAW.rds') bring back the simulated
# dat from an .rds file dfGRMSAAW <- readRDS('dfGRMSAAW.rds')If you save the .csv file (think “Excel lite”) and bring it back in, you will lose any formatting (e.g., ordered factors will be interpreted as character variables).
11.6 A Quick lavaan Syntax Recap
It’s really just regression
- tilda (~, is regressed on) is the regression operator
- place DV (y) on left side of the regression operator
- place IVs, separated by +, on the right of the regression operator
f is a latent variable (LV)
Example: y ~ f1 + f2 + x1 + x2
LVs must be defined by their manifest or latent indicators.
- the special operator (=~, is measured/defined by) is used for this
- Example: f1 =~ y1 + y2 + y3
Variances and covariances are specified with a double tilde operator (~~, is correlated with)
- Example of variance: y1 ~~ y1 (variable’s relationship with itself)
- Example of covariance: y1 ~~ y2 (relationship with another variable)
- Example of covariance of a factor: f1 ~~ f2
Intercepts (~ 1) for observed variables and LVs are simple, intercept-only regression formulas.
- Example of variable intercept: y1 ~ 1
- Example of factor intercept: f1 ~ 1
A complete lavaan model is a combination of these formula types, enclosed between single quotation marks. Readability of model syntax is improved by:
- splitting formulas over multiple lines
- using blank lines within single quote
- labeling with the hashtag
CFAmodel <- ’
f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9 + y10
’
Behind the scenes the cfa() function:
- fixes the factor loading of the first indicator of an LV to 1 (setting the scale)
- automatically adds residual variances (required)
- correlates all exogenous LVs; to turn these off add the following statement to the cfa() function statement: orthogonal = TRUE
11.7 Comparing and Tweaking Multidimensional First-Order Models
In the prior lesson we examined unidimensional and multidimensional variants of the GRMSAAW. Our work determined that the first-order structure that included four correlated factors was superior to a unidimensional measure. Starting with the multidimensional model (four factors), let’s specify both correlated and uncorrelated options and compare them. We’ll choose the best and see if we can further “tweak”” it into acceptable fit.
11.10 Model Respecification
Our correlated factors model has excellent fit, but this is not always the case. One way to improve model fit is to add parameters to simpler models – this is called model building. This can only occur for models that are overidentified (i.e., they have positive degrees of freedom).
In the CFA/psychometric case, a just-identified model is one that has at least 3 items per scale for a unidimensional factor structure and at least 2 items per scale in a multidimensional factor structure.
As we “free” each parameter (i.e., add paths or covariances), we correspondingly decrease the df. So, we must be diligent when engaging in model building.
In the CFA/psychometric case, freeing parameters usually means one of two things.
- Allowing cross-loadings.
- This would mean that an item belongs to two factors/scales. While this might be theoretically defensible, items that belong to more than one scale cause scoring difficulties when the scale is put into practice.
- Allowing the error variances of indicators to correlate.
- This would mean that there is something in common about the two items that is not explained/caused by the items’ relationship(s) with their respective factor(s). There are a variety of reasons this could occur, perhaps they have a content element that is in common, but different than the factor to which they belong. Methods factors (e.g., reverse scored items) can also contribute to items being correlated.
We use modification indices as a guide to determine if an error covariance is worth freeing. Modification indices tell you the degree to which your chi-square value will drop if the relationship between the two parameters is freed to relate (either a path or a covariance). Generally, a 1 degree of freedom change in a model will be a statistically significant difference if the chi-square value drops by 4 points. This is purely a statistical test that you have to then discern:
- if allowing the two elements to relate is theoretically defensible; and/or
- if there is truly something reasonably in common between the elements that is different from the theorized relations with the factors
Although many psychometricians frown on this, I think it, minimally, makes good diagnostic sense to take a look. The code below extracts the modification indices (MIs) from the object (corrF) that holds the lavaan output. Only MIs with a value greater than 4.0 are shown and they are sorted in descending order. We only ask for MIs greater than 4.0 because a 1 degree-of-freedom Chi-square difference test requires a difference of 3.841 (rounds to 4.0) to be statistically significant at \(p < 0.05\).
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
282 AF1 ~~ AUA1 8.812 -0.124 -0.124 -0.196 -0.196
324 MI2 ~~ MI3 8.166 0.135 0.135 0.206 0.206
275 AF1 ~~ AF3 7.785 0.115 0.115 0.195 0.195
69 AF =~ AS2 7.738 -0.435 -0.220 -0.218 -0.218
77 AF =~ MI1 7.221 0.517 0.261 0.313 0.313
120 AUA =~ MI5 6.740 0.537 0.297 0.337 0.337
95 MI =~ AF1 6.221 -0.539 -0.260 -0.290 -0.290
241 AS7 ~~ MI4 5.912 0.102 0.102 0.150 0.150
319 MI1 ~~ MI5 5.849 -0.092 -0.092 -0.166 -0.166
288 AF2 ~~ MI1 5.755 0.088 0.088 0.169 0.169
78 AF =~ MI2 5.748 -0.473 -0.239 -0.271 -0.271
193 AS4 ~~ MI4 5.479 -0.097 -0.097 -0.145 -0.145
289 AF2 ~~ MI2 5.191 -0.090 -0.090 -0.155 -0.155
163 AS3 ~~ AS5 5.059 -0.089 -0.089 -0.153 -0.153
124 AS1 ~~ AS5 5.050 0.085 0.085 0.156 0.156
168 AS3 ~~ AF1 4.910 0.082 0.082 0.143 0.143
112 AUA =~ AF1 4.850 -0.372 -0.206 -0.230 -0.230
113 AUA =~ AF2 4.735 0.416 0.230 0.237 0.237
278 AF1 ~~ MI2 4.601 -0.080 -0.080 -0.141 -0.141
63 AS =~ MI5 4.516 0.277 0.152 0.173 0.173
64 AS =~ AUA1 4.492 -0.349 -0.192 -0.188 -0.188
67 AS =~ AUA4 4.463 0.334 0.184 0.193 0.193
259 AS8 ~~ AUA3 4.441 -0.072 -0.072 -0.133 -0.133
182 AS4 ~~ AS6 4.380 -0.065 -0.065 -0.132 -0.132
92 MI =~ AS7 4.127 0.312 0.151 0.163 0.163
96 MI =~ AF2 4.072 0.494 0.238 0.245 0.24511.10.2 Respecifying with Crossloadings
Another route to improving model fit is to allow items to load on more than one factor (i.e., crossload). Let’s return to those original modification indices from the corrF specification.
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
282 AF1 ~~ AUA1 8.812 -0.124 -0.124 -0.196 -0.196
324 MI2 ~~ MI3 8.166 0.135 0.135 0.206 0.206
275 AF1 ~~ AF3 7.785 0.115 0.115 0.195 0.195
69 AF =~ AS2 7.738 -0.435 -0.220 -0.218 -0.218
77 AF =~ MI1 7.221 0.517 0.261 0.313 0.313
120 AUA =~ MI5 6.740 0.537 0.297 0.337 0.337
95 MI =~ AF1 6.221 -0.539 -0.260 -0.290 -0.290
241 AS7 ~~ MI4 5.912 0.102 0.102 0.150 0.150
319 MI1 ~~ MI5 5.849 -0.092 -0.092 -0.166 -0.166
288 AF2 ~~ MI1 5.755 0.088 0.088 0.169 0.169
78 AF =~ MI2 5.748 -0.473 -0.239 -0.271 -0.271
193 AS4 ~~ MI4 5.479 -0.097 -0.097 -0.145 -0.145
289 AF2 ~~ MI2 5.191 -0.090 -0.090 -0.155 -0.155
163 AS3 ~~ AS5 5.059 -0.089 -0.089 -0.153 -0.153
124 AS1 ~~ AS5 5.050 0.085 0.085 0.156 0.156
168 AS3 ~~ AF1 4.910 0.082 0.082 0.143 0.143
112 AUA =~ AF1 4.850 -0.372 -0.206 -0.230 -0.230
113 AUA =~ AF2 4.735 0.416 0.230 0.237 0.237
278 AF1 ~~ MI2 4.601 -0.080 -0.080 -0.141 -0.141
63 AS =~ MI5 4.516 0.277 0.152 0.173 0.173
64 AS =~ AUA1 4.492 -0.349 -0.192 -0.188 -0.188
67 AS =~ AUA4 4.463 0.334 0.184 0.193 0.193
259 AS8 ~~ AUA3 4.441 -0.072 -0.072 -0.133 -0.133
182 AS4 ~~ AS6 4.380 -0.065 -0.065 -0.132 -0.132
92 MI =~ AS7 4.127 0.312 0.151 0.163 0.163
96 MI =~ AF2 4.072 0.494 0.238 0.245 0.245The highest “factor to item” (as opposed to “item to item”) modification index is AF =~ AS2 . If we draw a path from AF to AS2, the overall chi-square will be reduced by 7.738 points. Recall, a 1 degree of freedom change in a model will be a statistically significant difference if the chi-square value drops by 4 points, so we can expect this to make a statistically significant difference.
In CFA models, allowing an item to load on more than one factor suggests that the item has something in common with both factors. Theoretically, this could make a great deal of sense. on, though, this creates confusion about scoring measures and interpreting them.
The item in question, AS2 reads, “Others have been surprised when I disagree with them.” Presently, it is assigned to the Ascribed Submissiveness factor. The MI is suggesting that it also be assigned to the Asian Fetishism scale.
In the context of this instrument whose CFA properties are already strong, I find it difficult to justify allowing these errors to covary, but I want to demonstrate the technique. We respecify it by adding AF1 to the MI factor.
ModInd_M2 <- "AS =~ AS1 + AS2 + AS3 + AS4 + AS5 + AS6 + AS7 + AS8 + AS9
AF =~ AF1 + AF2 + AF3 + AF4 + AS2
MI =~ MI1 + MI2 + MI3 + MI4 + MI5
AUA =~ AUA1 + AUA2 + AUA3 + AUA4
"set.seed(240311)
ModInd_M2f <- lavaan::cfa(ModInd_M2, data = dfGRMSAAW)
lavaan::summary(ModInd_M2f, fit.measures = TRUE, standardized = TRUE)lavaan 0.6.17 ended normally after 45 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 51
Number of observations 304
Model Test User Model:
Test statistic 224.190
Degrees of freedom 202
P-value (Chi-square) 0.136
Model Test Baseline Model:
Test statistic 1439.317
Degrees of freedom 231
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.982
Tucker-Lewis Index (TLI) 0.979
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -8276.884
Loglikelihood unrestricted model (H1) -8164.789
Akaike (AIC) 16655.768
Bayesian (BIC) 16845.336
Sample-size adjusted Bayesian (SABIC) 16683.590
Root Mean Square Error of Approximation:
RMSEA 0.019
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.032
P-value H_0: RMSEA <= 0.050 1.000
P-value H_0: RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.045
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
AS =~
AS1 1.000 0.544 0.593
AS2 1.437 0.194 7.424 0.000 0.781 0.774
AS3 0.974 0.125 7.806 0.000 0.530 0.564
AS4 0.913 0.121 7.514 0.000 0.496 0.536
AS5 1.149 0.135 8.536 0.000 0.625 0.638
AS6 0.675 0.095 7.124 0.000 0.367 0.501
AS7 0.835 0.119 7.032 0.000 0.454 0.493
AS8 0.913 0.121 7.542 0.000 0.496 0.539
AS9 0.760 0.105 7.221 0.000 0.413 0.510
AF =~
AF1 1.000 0.501 0.559
AF2 1.222 0.176 6.943 0.000 0.613 0.631
AF3 0.752 0.138 5.456 0.000 0.377 0.426
AF4 1.123 0.170 6.622 0.000 0.563 0.572
AS2 -0.480 0.181 -2.648 0.008 -0.240 -0.238
MI =~
MI1 1.000 0.481 0.577
MI2 0.916 0.148 6.200 0.000 0.441 0.500
MI3 1.171 0.177 6.597 0.000 0.564 0.551
MI4 0.924 0.157 5.872 0.000 0.445 0.463
MI5 0.690 0.137 5.021 0.000 0.332 0.377
AUA =~
AUA1 1.000 0.553 0.543
AUA2 0.981 0.140 7.018 0.000 0.543 0.608
AUA3 0.784 0.121 6.459 0.000 0.434 0.528
AUA4 1.083 0.152 7.146 0.000 0.599 0.630
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
AS ~~
AF 0.156 0.031 5.092 0.000 0.572 0.572
MI 0.140 0.028 4.997 0.000 0.534 0.534
AUA 0.182 0.034 5.302 0.000 0.607 0.607
AF ~~
MI 0.152 0.030 5.003 0.000 0.629 0.629
AUA 0.165 0.034 4.847 0.000 0.597 0.597
MI ~~
AUA 0.189 0.036 5.301 0.000 0.709 0.709
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.AS1 0.545 0.050 10.974 0.000 0.545 0.648
.AS2 0.566 0.063 9.029 0.000 0.566 0.555
.AS3 0.602 0.054 11.167 0.000 0.602 0.682
.AS4 0.610 0.054 11.324 0.000 0.610 0.712
.AS5 0.568 0.054 10.607 0.000 0.568 0.593
.AS6 0.402 0.035 11.496 0.000 0.402 0.749
.AS7 0.643 0.056 11.531 0.000 0.643 0.757
.AS8 0.602 0.053 11.310 0.000 0.602 0.710
.AS9 0.487 0.043 11.456 0.000 0.487 0.740
.AF1 0.552 0.055 10.047 0.000 0.552 0.687
.AF2 0.568 0.063 8.987 0.000 0.568 0.602
.AF3 0.639 0.057 11.232 0.000 0.639 0.818
.AF4 0.652 0.066 9.885 0.000 0.652 0.673
.MI1 0.466 0.047 9.826 0.000 0.466 0.668
.MI2 0.583 0.055 10.673 0.000 0.583 0.750
.MI3 0.730 0.072 10.152 0.000 0.730 0.697
.MI4 0.728 0.066 10.982 0.000 0.728 0.786
.MI5 0.665 0.058 11.515 0.000 0.665 0.858
.AUA1 0.730 0.069 10.536 0.000 0.730 0.705
.AUA2 0.502 0.051 9.795 0.000 0.502 0.630
.AUA3 0.487 0.046 10.679 0.000 0.487 0.721
.AUA4 0.545 0.058 9.475 0.000 0.545 0.603
AS 0.296 0.057 5.220 0.000 1.000 1.000
AF 0.251 0.057 4.403 0.000 1.000 1.000
MI 0.232 0.051 4.553 0.000 1.000 1.000
AUA 0.306 0.070 4.394 0.000 1.000 1.00011.10.2.1 Interpreting the Output
| Criteria | Our Results | Criteria met? |
|---|---|---|
| Factor loadings significant, strong, proper valence | AS:49. to .77; AF: -.24 to .63; MI: .38 to .58; AUA: .53 to .63 | No! When added to AF, AS1 is in the wrong direction |
| Non-significant chi-square | \(\chi ^{2}(202) = 224.190, p = 0.136\) | Yes |
| \(CFI\geq 0.982\) | CFI = 0.980 | Yes |
| \(RMSEA\leq .05\) (but definitely < .10) | RMSEA = 0.019, 90%CI(0.000, 0.032) | Yes |
| \(SRMR\leq .08\) (but definitely < .10) | SRMR = 0.045 | Yes |
| Combination rule: \(CFI \geq .95\) and \(SRMR \leq .08\) | CFI = 0.982, SRMR = 0.045 | Yes |
We can formally test the difference in models.
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
ModInd_M2f 202 16656 16845 224.19
corrF 203 16662 16848 232.45 8.2622 0.15456 1 0.004048 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1AIC and BIC are able to compare nested and non-nested models. Models with the lower values are superior. They both favor the model that allows AF1 to crossload on MI.
The \(\chi_{D}^{2}\) can only be used for nested models (where items/indicators are identical – the only difference is the presence/absence of parameters). If it is statistically significant, the better model is the one with the lower chi-square value. This, too, favors the correlated factors model, \(\chi ^{2}(1) = 8.262, p = 0.004\) .
Diagramming this model helps further clarify how we have specified this crossloading. It’s maybe tough to see, but AF1 now has arrows pointing from the AF and MI factors.
semPlot::semPaths(ModInd_M2f, layout = "tree", style = "lisrel", what = "col",
whatLabels = "stand")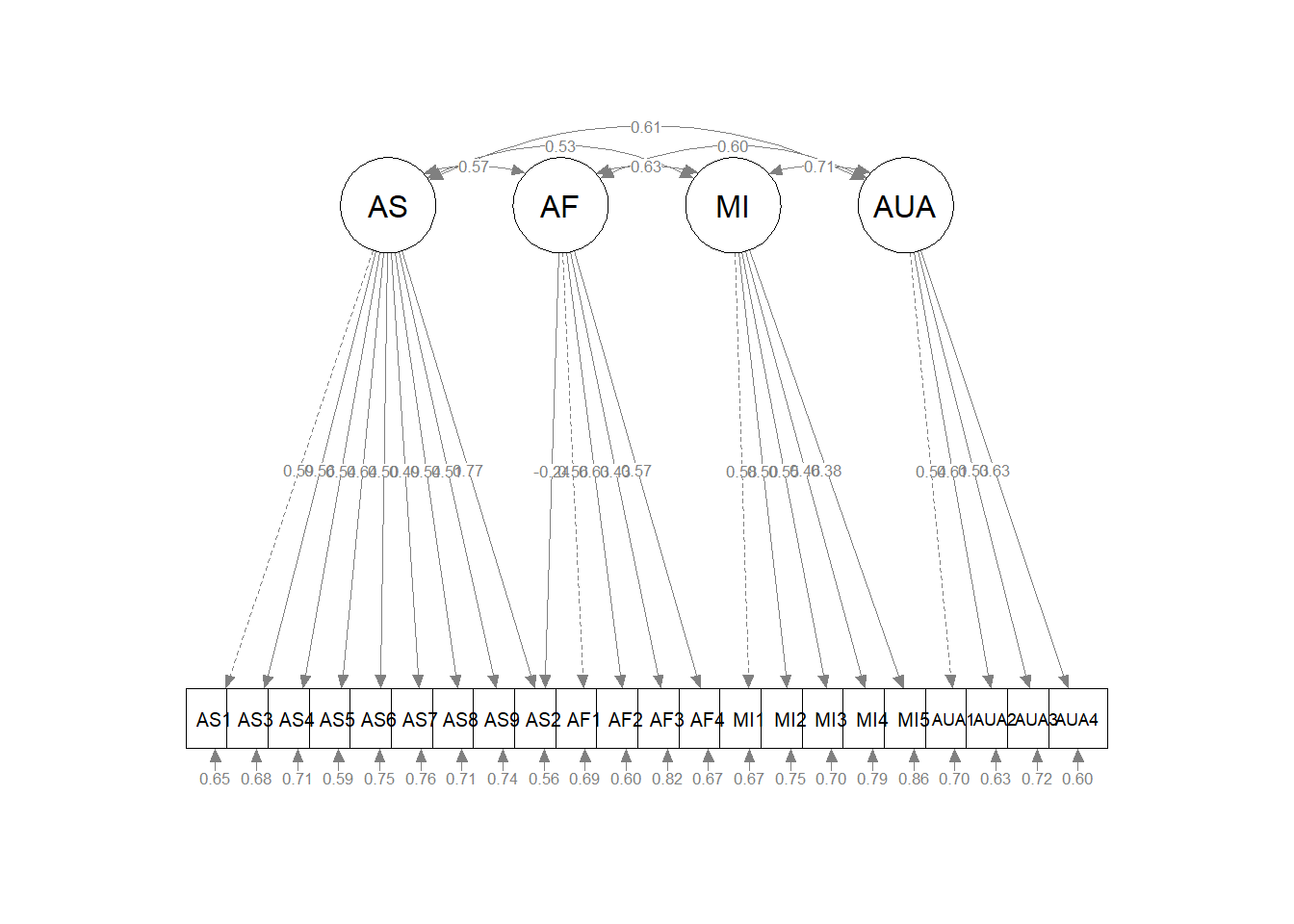 After each step, we should look again for modification indices.
After each step, we should look again for modification indices.
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
282 AF1 ~~ AUA1 9.276 -0.127 -0.127 -0.200 -0.200
324 MI2 ~~ MI3 8.250 0.135 0.135 0.207 0.207
275 AF1 ~~ AF3 7.525 0.113 0.113 0.190 0.190
77 AF =~ MI1 7.359 0.520 0.261 0.312 0.312
120 AUA =~ MI5 6.739 0.538 0.298 0.338 0.338
78 AF =~ MI2 6.647 -0.506 -0.254 -0.288 -0.288
124 AS1 ~~ AS5 6.220 0.094 0.094 0.169 0.169
319 MI1 ~~ MI5 5.868 -0.092 -0.092 -0.166 -0.166
241 AS7 ~~ MI4 5.828 0.101 0.101 0.148 0.148
288 AF2 ~~ MI1 5.707 0.087 0.087 0.169 0.169
193 AS4 ~~ MI4 5.463 -0.096 -0.096 -0.145 -0.145
95 MI =~ AF1 5.441 -0.492 -0.237 -0.264 -0.264
65 AS =~ AUA1 4.882 -0.372 -0.202 -0.199 -0.199
289 AF2 ~~ MI2 4.780 -0.086 -0.086 -0.149 -0.149
112 AUA =~ AF1 4.739 -0.367 -0.203 -0.226 -0.226
64 AS =~ MI5 4.561 0.286 0.156 0.177 0.177
259 AS8 ~~ AUA3 4.480 -0.072 -0.072 -0.133 -0.133
168 AS3 ~~ AF1 4.472 0.079 0.079 0.136 0.136
68 AS =~ AUA4 4.463 0.342 0.186 0.195 0.195
163 AS3 ~~ AS5 4.382 -0.082 -0.082 -0.140 -0.140
182 AS4 ~~ AS6 4.229 -0.064 -0.064 -0.129 -0.129
278 AF1 ~~ MI2 4.045 -0.075 -0.075 -0.132 -0.132Not surprisingly, these values continue to be quite low, and I would not propose that we make any of the modifications (not even the ones I have just demonstrated).
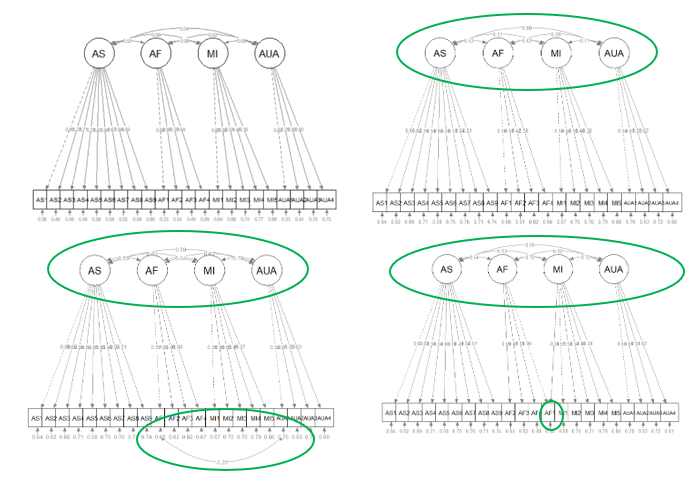
Looking at the models side-by-side, we can continue to think about the nested-to-nesting continuum. The uncorrF (upper left) model is nested (fewer specified parameters, higher degrees of freedom) in the corrF model (upper right). Our initial comparison was of these two models. We expected corrF to have superior fit, and it did!
We then compared the corrF model to the two models below. In these comparisons corrF was nested in each of the lower models which had one parameter freed (the error covariance on the lower left; the cross-loading on the lower right). As is common, each of these nesting models (more parameters, fewer degrees of freedom) had better fit. However, because the additions were not theoretically justifiable (and the fit for corrF was satisfatory), we did not retain these respecifications.
Think back to the don’t break the ice analogy – freeing all those parameters gets closer to the just-identified circumstance where all the relations in the sample covariance matrix are allowed to relate to each other (none are set to 0.0 or knocked out of the ice frame).
11.11 Modeling the GRMSAAW as a Second-Order Structure
Another approach to model building is to explore alternative factor structures. Let’s investigate a second-order model.
A second-order model represents the hypothesis that a second-order factor, g, causes each of the identified first-order factors. Note that:
- The first-order factors have indicators, but the general factor has none; that is, the second-order factor is measured only indirectly through the indicators of the first-order factors.
- The specification of g as a common cause of the lower order factors implies that any additional association between the first-order factors is spurious.
- There must be at least three first-order factors or their disturbance variances may be underidentified;
- each first-order factor should have at least two indicators; more is better
- There are two options for scaling g:
- fixing the direct of effect of g on one factor (usually the first or last) to 1.0; or
- fixing the variance of g to 1.0 (standardizing it); this leaves all direct effects of g on the first-order factors as free parameters.
In our second-order model, we will add an the overall GRMS factor as our g below the four existing factors.
secondM <- "AS =~ AS1 + AS2 + AS3 + AS4 + AS5 + AS6 + AS7 + AS8 + AS9
AF =~ AF1 + AF2 + AF3 + AF4
MI =~ MI1 + MI2 + MI3 + MI4 + MI5
AUA =~ AUA1 + AUA2 + AUA3 + AUA4
GRMS =~ AS + AF + MI + AUA"Next, we extract the results from the secondM object with the lavaan::cfa() function.
set.seed(240311)
secondF <- lavaan::cfa(secondM, data = dfGRMSAAW)
lavaan::summary(secondF, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)lavaan 0.6.17 ended normally after 41 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 48
Number of observations 304
Model Test User Model:
Test statistic 234.741
Degrees of freedom 205
P-value (Chi-square) 0.076
Model Test Baseline Model:
Test statistic 1439.317
Degrees of freedom 231
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.975
Tucker-Lewis Index (TLI) 0.972
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -8282.159
Loglikelihood unrestricted model (H1) -8164.789
Akaike (AIC) 16660.319
Bayesian (BIC) 16838.736
Sample-size adjusted Bayesian (SABIC) 16686.504
Root Mean Square Error of Approximation:
RMSEA 0.022
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.034
P-value H_0: RMSEA <= 0.050 1.000
P-value H_0: RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.047
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
AS =~
AS1 1.000 0.549 0.598
AS2 1.138 0.137 8.326 0.000 0.625 0.618
AS3 0.959 0.124 7.740 0.000 0.526 0.560
AS4 0.902 0.121 7.475 0.000 0.495 0.535
AS5 1.154 0.134 8.589 0.000 0.633 0.647
AS6 0.674 0.094 7.142 0.000 0.370 0.505
AS7 0.833 0.118 7.043 0.000 0.457 0.496
AS8 0.908 0.120 7.539 0.000 0.498 0.541
AS9 0.759 0.105 7.242 0.000 0.417 0.514
AF =~
AF1 1.000 0.506 0.564
AF2 1.193 0.174 6.847 0.000 0.603 0.621
AF3 0.740 0.137 5.402 0.000 0.374 0.423
AF4 1.134 0.171 6.644 0.000 0.573 0.582
MI =~
MI1 1.000 0.476 0.570
MI2 0.937 0.151 6.197 0.000 0.446 0.505
MI3 1.201 0.182 6.590 0.000 0.571 0.558
MI4 0.928 0.160 5.798 0.000 0.442 0.459
MI5 0.698 0.140 4.992 0.000 0.332 0.377
AUA =~
AUA1 1.000 0.550 0.541
AUA2 0.988 0.141 6.988 0.000 0.544 0.609
AUA3 0.788 0.123 6.427 0.000 0.434 0.528
AUA4 1.091 0.153 7.112 0.000 0.600 0.631
GRMS =~
AS 1.000 0.683 0.683
AF 1.001 0.184 5.450 0.000 0.742 0.742
MI 1.033 0.183 5.657 0.000 0.814 0.814
AUA 1.244 0.222 5.594 0.000 0.847 0.847
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.AS1 0.540 0.050 10.844 0.000 0.540 0.642
.AS2 0.630 0.059 10.679 0.000 0.630 0.618
.AS3 0.606 0.055 11.116 0.000 0.606 0.687
.AS4 0.611 0.054 11.264 0.000 0.611 0.714
.AS5 0.558 0.054 10.413 0.000 0.558 0.582
.AS6 0.400 0.035 11.421 0.000 0.400 0.745
.AS7 0.640 0.056 11.463 0.000 0.640 0.754
.AS8 0.600 0.053 11.230 0.000 0.600 0.708
.AS9 0.484 0.043 11.377 0.000 0.484 0.736
.AF1 0.548 0.055 9.902 0.000 0.548 0.682
.AF2 0.579 0.064 9.040 0.000 0.579 0.614
.AF3 0.641 0.057 11.212 0.000 0.641 0.821
.AF4 0.640 0.066 9.652 0.000 0.640 0.661
.MI1 0.471 0.048 9.902 0.000 0.471 0.676
.MI2 0.579 0.055 10.611 0.000 0.579 0.744
.MI3 0.722 0.072 10.051 0.000 0.722 0.689
.MI4 0.731 0.066 11.000 0.000 0.731 0.789
.MI5 0.665 0.058 11.510 0.000 0.665 0.858
.AUA1 0.733 0.070 10.552 0.000 0.733 0.708
.AUA2 0.500 0.051 9.760 0.000 0.500 0.629
.AUA3 0.488 0.046 10.671 0.000 0.488 0.722
.AUA4 0.544 0.058 9.439 0.000 0.544 0.601
.AS 0.160 0.036 4.499 0.000 0.533 0.533
.AF 0.115 0.034 3.342 0.001 0.449 0.449
.MI 0.076 0.028 2.750 0.006 0.337 0.337
.AUA 0.085 0.034 2.505 0.012 0.282 0.282
GRMS 0.140 0.036 3.877 0.000 1.000 1.000
R-Square:
Estimate
AS1 0.358
AS2 0.382
AS3 0.313
AS4 0.286
AS5 0.418
AS6 0.255
AS7 0.246
AS8 0.292
AS9 0.264
AF1 0.318
AF2 0.386
AF3 0.179
AF4 0.339
MI1 0.324
MI2 0.256
MI3 0.311
MI4 0.211
MI5 0.142
AUA1 0.292
AUA2 0.371
AUA3 0.278
AUA4 0.399
AS 0.467
AF 0.551
MI 0.663
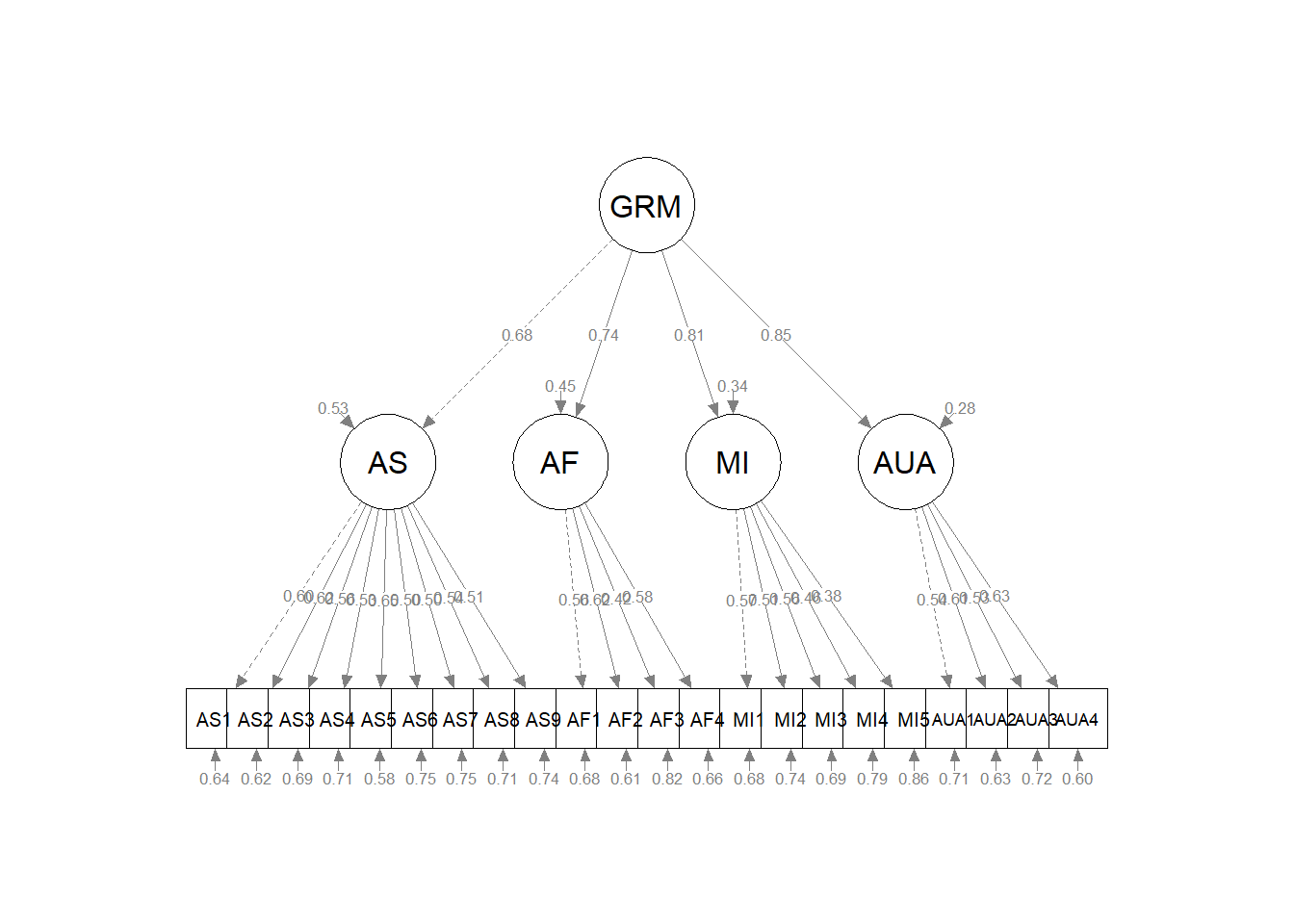
AUA 0.718As we plot this model we expect to see a “second level” factor predicting each of the “first order” factors. The indicator was set on GRM –> AS. Each of the four factors predicts only the items associated with their factor with one item for each factor (the first on the left) specified as the indicator variable.
 Again, among my first steps are also to write the code to export the results. The tidySEM package has useful functions to export the fit statistics, parameter estimates, and correlations among the latent variables (i.e., factors).
Again, among my first steps are also to write the code to export the results. The tidySEM package has useful functions to export the fit statistics, parameter estimates, and correlations among the latent variables (i.e., factors).
secondFFitStats <- tidySEM::table_fit(secondF)
secondF_paramEsts <- tidySEM::table_results(secondF, digits=3, columns = NULL)
#because of the second order, there are no correlations among the LVs to request
#to see each of the tables, remove the hashtab
#secondFFitStats
#secondF_paramEstsNext, I export them.
write.csv(secondFFitStats, file = "secondFFitStats.csv")
write.csv(secondF_paramEsts, file = "secondF_paramEsts.csv")11.11.1 Interpreting the Output
| Criteria | Our Results | Criteria met? |
|---|---|---|
| Factor loadings significant, strong, proper valence | AS: .50 to .65; AF: .42 to .62; MI: .38 to .57; AUA: .53 to .63; GRMS: .68 to .85 | Yes |
| Non-significant chi-square | \(\chi ^{2}(205) = 234.741, p = 0.076\) | Yes |
| \(CFI\geq .95\) | CFI = 0.975 | Yes |
| \(RMSEA\leq .05\) (but definitely < .10) | RMSEA = 0.022, 90%CI(0.000, 0.034) | Yes |
| \(SRMR\leq .08\) (but definitely < .10) | SRMR = 0.047 | Yes |
| Combination rule: \(CFI \geq .95\) and \(SRMR \leq .08\) | CFI = 0.975 , SRS = 0.047 | Yes |
11.11.2 Partial Write-up
Second-order factor model. Our next model represented a second order structure. Specifically, four first-order factors loaded onto a second factor model and demonstrated adequate fit to the data: \(\chi ^{2}(205) = 234.741, p = 0.076, CFI = 0.975, RMSEA = 0.022, 90%CI(0.000, 0.034), SRMR = .047\). Factor loadings ranged from .50 to .65 for the AS scale, .42 to .62 for the AF scale, .38 to .57 for the MI scale, .53 to .63 for the AUA scale, and .68 to .85 for the GRMS total scale.
Determining if models are nested vs. hierarchically arranged can be confusing, especially when it comes to adding in second-order structures. That is, replacing the six correlations (in the correlated factors model) with the second-order factor (fixing the first of the first-order factors to 1.0, so adding only 3 paths to be estimated) is not a clear fixing or freeing of paths. We need to know if they are so that we know if it is appropriate to apply/interpret the \(\chi_{D}^{2}\) difference test.
Luckily, the Muthen’s (creators of Mplus) have a discussion post devoted to this and it appears that our correlated factors model is the nesting model for the second-order structure. If there is a statistically significant difference in models, then the correlated factors model is superior.
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
corrF 203 16662 16848 232.45
secondF 205 16660 16839 234.74 2.289 0.02178 2 0.3185
uncorrF 209 16879 17042 461.10 226.361 0.42762 4 <0.0000000000000002
corrF
secondF
uncorrF ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Although there is not a statistically significant chi-square difference (\(\chi^{2}(2) = .37923, p = .827\) between the correlated factors and second order structure, the AIC and BIC favor (by a very small amount) the second-order model.
If our model fit was poor, we would want to inspect the modification indices and see if it would be justifiable to allow error covariances.
lhs op rhs mi epc sepc.lv sepc.all sepc.nox
303 AF1 ~~ AUA1 9.880 -0.131 -0.131 -0.207 -0.207
137 GRMS =~ MI5 9.635 1.388 0.520 0.591 0.591
76 AF =~ MI1 8.672 0.519 0.262 0.314 0.314
296 AF1 ~~ AF3 7.683 0.115 0.115 0.194 0.194
345 MI2 ~~ MI3 7.464 0.129 0.129 0.200 0.200
68 AF =~ AS2 7.396 -0.410 -0.207 -0.205 -0.205
119 AUA =~ MI5 6.946 0.525 0.289 0.328 0.328
129 GRMS =~ AF1 6.925 -0.953 -0.357 -0.399 -0.399
130 GRMS =~ AF2 6.303 1.048 0.393 0.405 0.405
111 AUA =~ AF1 6.125 -0.450 -0.248 -0.277 -0.277
309 AF2 ~~ MI1 5.928 0.088 0.088 0.169 0.169
262 AS7 ~~ MI4 5.764 0.101 0.101 0.148 0.148
214 AS4 ~~ MI4 5.745 -0.099 -0.099 -0.149 -0.149
121 GRMS =~ AS2 5.427 -0.614 -0.230 -0.228 -0.228
340 MI1 ~~ MI5 5.391 -0.089 -0.089 -0.158 -0.158
145 AS1 ~~ AS5 5.270 0.087 0.087 0.159 0.159
94 MI =~ AF1 5.171 -0.467 -0.222 -0.248 -0.248
189 AS3 ~~ AF1 5.066 0.084 0.084 0.145 0.145
184 AS3 ~~ AS5 4.864 -0.087 -0.087 -0.150 -0.150
310 AF2 ~~ MI2 4.801 -0.086 -0.086 -0.148 -0.148
77 AF =~ MI2 4.730 -0.400 -0.202 -0.230 -0.230
66 AS =~ AUA4 4.512 0.316 0.173 0.182 0.182
203 AS4 ~~ AS6 4.441 -0.066 -0.066 -0.133 -0.133
280 AS8 ~~ AUA3 4.375 -0.071 -0.071 -0.131 -0.131
95 MI =~ AF2 4.349 0.479 0.228 0.235 0.235
299 AF1 ~~ MI2 4.174 -0.075 -0.075 -0.134 -0.134
69 AF =~ AS3 4.137 0.294 0.148 0.158 0.158
80 AF =~ MI5 4.006 0.367 0.185 0.211 0.211The same AF1 ~~ AUA1 relationship is showing as the item that has a larger modification index than the others. As we saw earlier, freeing it to covary would improve the fit. However, our more parsimonious models (correlated factors, second-order) have excellent fit. Therefore, we will not respecify at this time.
11.12 Modeling the GRMSAAW as a Bifactor Model
Bifactor models are also known as nested-factor and general-specific models. Like the second-order model, they involve several specific, correlated constructs that make up a more general construct of interest. The big difference:
- g in the bifactor model directly affects the indicators but is orthogonal/unrelated to the specific factors
- bifactor models where g covaries with the specific factors may not be identified
- bifactor models partition variance into three nonoverlapping sources:
- specific factors
- the general factor (g)
- error
Second-order and bifactor models make very different assumptions about whether g is unrelated to the other factors (bifactor model) or covaries with/mediates those other factors (second-order model).
Take note that the base factor structure for the bifactor model is identical to the second-order structure. The difference is that the script fixes the relations between g and each of the factors to 0.0; and the relations between each of the factors to each other as 0.0.
bifacM <- " GRMS =~ AS1 + AS2 + AS3 + AS4 + AS5 + AS6 + AS7 + AS8 + AS9 + AF1 + AF2 + AF3 + AF4 + MI1 + MI2 + MI3 + MI4 + MI5 + AUA1 + AUA2 + AUA3 + AUA4
AS =~ AS1 + AS2 + AS3 + AS4 + AS5 + AS6 + AS7 + AS8 + AS9
AF =~ AF1 + AF2 + AF3 + AF4
MI =~ MI1 + MI2 + MI3 + MI4 + MI5
AUA =~ AUA1 + AUA2 + AUA3 + AUA4
#fixes the relations between g and each of the factors to 0.0
GRMS ~~ 0*AS
GRMS ~~ 0*AF
GRMS ~~ 0*MI
GRMS ~~ 0*AUA
#fixes the relations (covariances) between each of the factors to 0.0
AS ~~ 0*AF
AS ~~ 0*MI
AS ~~ 0*AUA
AF ~~ 0*MI
AF ~~ 0*AUA
MI ~~ 0*AUA
"# On the first run I received a warning; it is not uncommon to add
# the statement 'check.gradient=FALSE' to force a solution. Then it
# is important to closely inspect the results to see if things look
# ok. If you get really stuck it is possible to change optimizers
# through control statements
set.seed(240311)
bifacF <- lavaan::cfa(bifacM, data = dfGRMSAAW, check.gradient = FALSE)
lavaan::summary(bifacF, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)lavaan 0.6.17 ended normally after 100 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 66
Number of observations 304
Model Test User Model:
Test statistic 191.208
Degrees of freedom 187
P-value (Chi-square) 0.401
Model Test Baseline Model:
Test statistic 1439.317
Degrees of freedom 231
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.997
Tucker-Lewis Index (TLI) 0.996
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -8260.393
Loglikelihood unrestricted model (H1) -8164.789
Akaike (AIC) 16652.786
Bayesian (BIC) 16898.110
Sample-size adjusted Bayesian (SABIC) 16688.791
Root Mean Square Error of Approximation:
RMSEA 0.009
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.027
P-value H_0: RMSEA <= 0.050 1.000
P-value H_0: RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.039
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
GRMS =~
AS1 1.000 0.363 0.396
AS2 0.907 0.192 4.719 0.000 0.329 0.326
AS3 1.089 0.209 5.204 0.000 0.395 0.421
AS4 0.917 0.191 4.789 0.000 0.333 0.359
AS5 1.231 0.219 5.616 0.000 0.447 0.456
AS6 0.779 0.160 4.880 0.000 0.283 0.386
AS7 1.077 0.213 5.060 0.000 0.391 0.424
AS8 0.936 0.193 4.847 0.000 0.340 0.369
AS9 0.650 0.157 4.149 0.000 0.236 0.291
AF1 0.877 0.212 4.136 0.000 0.318 0.355
AF2 1.432 0.278 5.149 0.000 0.520 0.535
AF3 0.765 0.200 3.829 0.000 0.278 0.314
AF4 1.215 0.256 4.744 0.000 0.441 0.448
MI1 1.154 0.231 5.001 0.000 0.419 0.501
MI2 0.884 0.211 4.199 0.000 0.321 0.364
MI3 1.109 0.253 4.380 0.000 0.402 0.393
MI4 0.956 0.228 4.196 0.000 0.347 0.361
MI5 0.992 0.220 4.504 0.000 0.360 0.409
AUA1 1.211 0.264 4.580 0.000 0.439 0.432
AUA2 1.235 0.250 4.947 0.000 0.448 0.502
AUA3 0.979 0.213 4.596 0.000 0.355 0.432
AUA4 1.509 0.288 5.240 0.000 0.547 0.576
AS =~
AS1 1.000 0.416 0.453
AS2 1.398 0.252 5.548 0.000 0.581 0.575
AS3 0.815 0.183 4.464 0.000 0.339 0.360
AS4 0.899 0.191 4.718 0.000 0.374 0.404
AS5 1.056 0.203 5.201 0.000 0.439 0.448
AS6 0.571 0.140 4.080 0.000 0.238 0.324
AS7 0.588 0.167 3.520 0.000 0.245 0.265
AS8 0.861 0.187 4.617 0.000 0.358 0.389
AS9 0.867 0.177 4.892 0.000 0.360 0.444
AF =~
AF1 1.000 0.620 0.691
AF2 0.342 0.162 2.108 0.035 0.212 0.218
AF3 0.446 0.196 2.270 0.023 0.276 0.312
AF4 0.474 0.207 2.293 0.022 0.294 0.298
MI =~
MI1 1.000 0.190 0.227
MI2 1.874 0.766 2.446 0.014 0.355 0.403
MI3 2.959 1.340 2.208 0.027 0.561 0.548
MI4 1.326 0.610 2.174 0.030 0.251 0.261
MI5 -0.043 0.401 -0.107 0.915 -0.008 -0.009
AUA =~
AUA1 1.000 0.419 0.412
AUA2 0.794 0.370 2.147 0.032 0.333 0.373
AUA3 0.590 0.275 2.145 0.032 0.247 0.301
AUA4 0.444 0.245 1.813 0.070 0.186 0.196
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
GRMS ~~
AS 0.000 0.000 0.000
AF 0.000 0.000 0.000
MI 0.000 0.000 0.000
AUA 0.000 0.000 0.000
AS ~~
AF 0.000 0.000 0.000
MI 0.000 0.000 0.000
AUA 0.000 0.000 0.000
AF ~~
MI 0.000 0.000 0.000
AUA 0.000 0.000 0.000
MI ~~
AUA 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.AS1 0.536 0.050 10.644 0.000 0.536 0.638
.AS2 0.574 0.064 8.986 0.000 0.574 0.563
.AS3 0.612 0.054 11.277 0.000 0.612 0.693
.AS4 0.606 0.054 11.129 0.000 0.606 0.708
.AS5 0.566 0.054 10.518 0.000 0.566 0.591
.AS6 0.401 0.035 11.531 0.000 0.401 0.746
.AS7 0.637 0.055 11.605 0.000 0.637 0.750
.AS8 0.605 0.054 11.220 0.000 0.605 0.713
.AS9 0.472 0.044 10.829 0.000 0.472 0.718
.AF1 0.318 0.156 2.041 0.041 0.318 0.396
.AF2 0.628 0.059 10.673 0.000 0.628 0.666
.AF3 0.628 0.060 10.552 0.000 0.628 0.804
.AF4 0.688 0.067 10.333 0.000 0.688 0.710
.MI1 0.486 0.045 10.741 0.000 0.486 0.697
.MI2 0.548 0.067 8.199 0.000 0.548 0.705
.MI3 0.572 0.132 4.333 0.000 0.572 0.546
.MI4 0.742 0.067 11.024 0.000 0.742 0.802
.MI5 0.646 0.057 11.354 0.000 0.646 0.833
.AUA1 0.667 0.097 6.904 0.000 0.667 0.644
.AUA2 0.484 0.063 7.679 0.000 0.484 0.608
.AUA3 0.488 0.049 9.917 0.000 0.488 0.723
.AUA4 0.570 0.055 10.420 0.000 0.570 0.630
GRMS 0.132 0.043 3.053 0.002 1.000 1.000
AS 0.173 0.051 3.399 0.001 1.000 1.000
AF 0.384 0.165 2.327 0.020 1.000 1.000
MI 0.036 0.026 1.373 0.170 1.000 1.000
AUA 0.176 0.100 1.752 0.080 1.000 1.000
R-Square:
Estimate
AS1 0.362
AS2 0.437
AS3 0.307
AS4 0.292
AS5 0.409
AS6 0.254
AS7 0.250
AS8 0.287
AS9 0.282
AF1 0.604
AF2 0.334
AF3 0.196
AF4 0.290
MI1 0.303
MI2 0.295
MI3 0.454
MI4 0.198
MI5 0.167
AUA1 0.356
AUA2 0.392
AUA3 0.277
AUA4 0.370Providing a traditional diagram of the bifactor model requires some extra steps. The default from semPlot’s semPaths() function produces this:
 While it is an accurate depiction, I was seeking the traditional illustration. I found some instructive discussion on Sacha Epskamp’s semPlot repo on GitHub.
While it is an accurate depiction, I was seeking the traditional illustration. I found some instructive discussion on Sacha Epskamp’s semPlot repo on GitHub.
We can think of the variables in our model as numbered. The items take the first numbers, followed by g, and then each of the factors. We need to represent them in a matrix of 0s and numbers. Let’s start by mapping them out. The top row is the factors (4), the second row is items (22), the bottom row is g (1)
[1, ] 0 0 0 24 0 0 0 0 25 0 0 0 0 0 26 0 0 0 0 0 27 0 0 [2, ] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 [3, ] 0 0 0 0 0 0 0 0 0 0 0 0 28 0 0 0 0 0 0 0 0 0 0
m = matrix(nrow = 3, ncol = 22)
m[1, ] = c(0, 0, 0, 0, 24, 0, 0, 0, 0, 0, 25, 0, 0, 0, 0, 26, 0, 0, 0,
0, 27, 0)
m[2, ] = 1:22
m[3, ] = c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 23, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0)
m [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
[1,] 0 0 0 0 24 0 0 0 0 0 25 0 0 0
[2,] 1 2 3 4 5 6 7 8 9 10 11 12 13 14
[3,] 0 0 0 0 0 0 0 0 0 0 0 23 0 0
[,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
[1,] 0 26 0 0 0 0 27 0
[2,] 15 16 17 18 19 20 21 22
[3,] 0 0 0 0 0 0 0 0 Among my first steps are also to write the code to export the results. The tidySEM package has useful functions to export the fit statistics, parameter estimates, and correlations among the latent variables (i.e., factors).
Among my first steps are also to write the code to export the results. The tidySEM package has useful functions to export the fit statistics, parameter estimates, and correlations among the latent variables (i.e., factors).
bifacFFitStats <- tidySEM::table_fit(bifacF)
bifacF_paramEsts <- tidySEM::table_results(bifacF, digits=3, columns = NULL)
bifacFCorrs <- tidySEM::table_cors(bifacF, digits=3)
#to see each of the tables, remove the hashtab
#bifacFFitStats
#bifacF_paramEsts
#bifacFCorrsNext, I export them.
write.csv(bifacFFitStats, file = "bifacFFitStats.csv")
write.csv(bifacF_paramEsts, file = "bifacF_paramEsts.csv")
write.csv(bifacFCorrs, file = "bifacFCorrs.csv")Troubleshooting tip: If, while working with this function you get the error: “Error in file(file, ifelse(append,”a”, “w”)) : cannot open the connection”, it’s because the .csv file that received your table is still open. R is just trying to write over it. A similar error happens when knitting.
11.12.1 Interpreting the Output
| Criteria | Our Results | Criteria met? |
|---|---|---|
| Factor loadings significant, strong, proper valence | GRMS: .29 to .58; AS: .27 to .58; AF: .22 to .69; MI: -.01 to .55; AUA: .20 to .41 | |
| MI5 is near-zero and negative | ||
| Non-significant chi-square | \(\chi ^{2}(187) = 191.208, p = 0.401\) | Yes |
| \(CFI\geq .95\) | CFI = 0.997 | Yes |
| \(RMSEA\leq .05\) (but definitely < .10) | RMSEA = 0.009, 90%CI(0.000, 0.027 | Yes |
| \(SRMR\leq .08\) (but definitely < .10) | SRMR = 0.039 | Yes |
| Combination rule: \(CFI \geq .95\) and \(SRMR \leq .08\) | CFI = 0.997, SRS = 0.039 | Yes |
As promised, even in spite of the wiggly factor loadings, the model fit improves. This is another example of the nesting model generally having the best fit.
11.12.2 Partial Write-up
Bifactor model. The bifactor model regressed each item on its respective factor while simultaneously regressing each indicator onto an overall GRMS scale. This model had the best fit of those compared thus far: \(\chi ^{2}(187) = 164.080, p = .885\), CFI = 0.997 , RMSEA = 0.009, 90%CI(0.000, 0.027), SRMR = 0.039. Factor loadings for the four factors ranged from .27 to .58 for the AS scale, .22 to .69 for the AF scale, -.01 to .55 for the MI scale, and .20 to .41 for the AUA scale. Factor loadings for the overall GRMSAAW (g) ranged from .29 to .58.
On the basis of this evaluation, we are finding all four models to be satisfactory (in terms of fit): the single-order uncorrelated factors (uncorrF), the single-order correlated factors model (corrF), the second order factor (secondF), and the bifactor model (bifacF). We can use lavaan’s lavTest() function to compare them. No matter the order that we enter them, the function orders them according to their degrees of freedom.
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
bifacF 187 16653 16898 191.21
corrF 203 16662 16848 232.45 41.244 0.07204 16 0.000511
secondF 205 16660 16839 234.74 2.289 0.02178 2 0.318460
uncorrF 209 16879 17042 461.10 226.361 0.42762 4 < 0.00000000000000022
bifacF
corrF ***
secondF
uncorrF ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We see that the bifacF and corrF models are statistically significantly different from each other. The AIC favors the bifacF; the BIC favors the corrF. We may be interested in knowing how it compares to the secondF model. The two models are statistically significantly different. The lower value of the AIC favors the bifactor model; the lower value of the BIC favors the second-order model.
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
bifacF 187 16653 16898 191.21
secondF 205 16660 16839 234.74 43.533 0.068309 18 0.0006725 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1In the article, Keum et al. (2018) reported the best fit for the bifactor model. They reported strong, significant, and properly valanced loadings for the g factor as well as for each of the group factors. Our wiggly factor loadings on g and the MI scale are likely an artifact of simulating the data from the EFA factor loadings.
11.13 Another Look at Omega
Now that we’ve had an introduction to CFA/SEM – and the second-order and bifactor models in particular – let’s look again the \(\omega\) grouping of reliability estimates.
In prior lessons we used the psych package’s omegaSem() function with raw data. The package estimated a family of model-based estimates that examine the correlations or covariances of the items and decomposed the test variance into that which is
- common to all items (g, a general factor),
- specific to some items (f, orthogonal group factors), and
- unique to each item (confounding s specific, and e error variance).
When using raw data or a correlation matrix as the object for the omega analysis, it is possible to specify the number of factors, but the procedure is exploratory and there is no guarantee that the items will associate with the intended factor. When we are concerned with the omega reliability estimates for clearly specified factor structure we can feed our lavaan::cfa models to semTools::reliability() function and obtain the estimates.
11.13.1 Omega h for Bifactor Models
In bifactor models the general factor captures the variance common across all items and the specific factors account for what is left over. Specific factors represent what is common across members of that factor, separate from what is claimed by g.
In the context of a bifactor model, the reliability measure, \(\omega_{h}\), represents the proportion of total-score variance due to a single, general construct that influences all items, despite the multidimensional nature of the item set (Flora, 2020a, 2020b).
Stated in terms of the GRMSAAW, \(\omega_{h}\) represents the extent to which the GRMSAAW total score provides a reliable measure of a construct represented by a general factor that influences all items in a multidimensional scale over and above the AS, AF, MI, and AUA subscales.
If we use the semTools::reliability() function, we pass it the object we created from our lavaan::cfa(). Flora’s article and supplementary materials (Flora, 2020a, 2020b) provide an excellent description and review of how to specify and interpret \(\omega_{h}\) with semTools::reliability().
GRMS AS AF MI AUA total
alpha 0.8485768 0.8015849 0.6327835 0.6130925 0.6665705 0.8485768
omega 0.8469630 0.6910784 0.4645562 0.3778777 0.3888254 0.8725861
omega2 0.7051557 0.4323840 0.2953065 0.2210012 0.2061386 0.8725861
omega3 0.7059886 0.4324453 0.2949845 0.2193985 0.2060547 0.8736167
avevar NA NA NA NA NA 0.3285899In the case of the bifactor model, the estimates listed under the GRMS column pertain to the general GRMS factor. We typically focus on the omega2 and omega3 values as the indicators of \(\omega_{h}\). Flora (2020a) indicates that omega2 is calculated using the model-implied variance of the total score in its denominator and omega3 is calculated using the observed sample variance of X. To the degree that these two values are different from each other, we may have concerns. In our data, omega2 = 0.705 and omega3 = 0.706. These values indicate the proportion of GRMS total-score variance that is due to a general factor, over-and-above, the influence of effects that are specific to the group factors (i.e., AS, AF, MI, AUA).
The omega2 and omega3 values in the AS through AUA columns are the omega-hierarchical-subscale. These analyses indicate how well a given subscale reliably measures a narrower construct that is independent from the broader higher-order construct that also influences the other subscales. Flora (2020b) notates these as \(\omega_{h-ss}\) (omega-higherarchical-subscale). Specifically, \(\omega_{h-ss}\) represents the proportion of variance in a subscale that is due to the coresponding specific factor, over and above the influence of the general factor. Comparing the relative values to each other can provide some indication of the source of reliable variance. We see that the AS, AF, and AUA factors are considerably lower than the GRMS, however they are holding their own. Taken together, the omega values from our bifactor model suggest a strong general factor with subscales that are meaningful and useful. Our results paralleled the pattern reported in Keum et al. (2018). In their follow-up investigation of construct validity, they used structural equation modeling with the bifactor model to investigate the relationships between the GRMSAAW with relevant constructs.
In bifactor models, the multidimensionality of items (i.e., the existence of factors) is considered to be a “nuisance” (Flora, 2020b) for the measurement of a broad, general construct. This is different from hierarchical models such as the second-order factor structure. Since we can calculate \(\omega_{h}\) for it, let’s look at it, next.
11.13.2 \(\omega_{h}\) for Second Order Models
In the second-order structure, the researcher hypothesizes that there is a broad, overarching construct indirectly influencing all items in a test through more conceptually narrow constructs that directly influence different groupings of items. This hypothesis implies that item-level data arise from a higher order model, in which the second-order factor, causes individual differences in the first-order factor, which directly influences the observed item responses.
In this case, \(\omega_{ho}\) (ho = higher order) (Flora, 2020b) represents the proportion of total-score variance that is due to the higher-order factor. As such, it represents the reliability of a total score for measuring a single construct that influences all items.
To use semTools we switch functions to reliabilityL2. The specification
omegaL1 omegaL2 partialOmegaL1
0.7038702 0.8547458 0.8420019 The estimate listed under omegaL1 (\(\omega_{ho}\)) represents the proportion of GRMSAAW total score variance due to the higher-order factor. The value of 0.704 is consistent with what we saw in the bifactor model.
We can apply the semTools::reliability() function to the R object that holds the second-order results to obtain omega values for the subscales. Below the alpha coefficients, the omega values indicate how reliably each subscale measures its lower order factor. For example, 80% of the total variance of a total score comprised of only the 9 items in the AS scale is explained by the AS lower order factor.
AS AF MI AUA
alpha 0.8015849 0.6327835 0.6130925 0.6665705
omega 0.8045496 0.6370410 0.6184523 0.6666061
omega2 0.8045496 0.6370410 0.6184523 0.6666061
omega3 0.8052908 0.6352363 0.6193718 0.6637510
avevar 0.3194991 0.3111493 0.2500576 0.3361644Using the omega2 values, the subscale omegas range from .62 to .80. It is helpful to see how the omega values align with the alpha coefficients.
11.13.3 Partial Write-up
Given that we landed on the bifactor model as our final solution, here’s how I might represent the omega results.
As estimates of model-based internal consistency associated with the bifactor model, we calculated omega hierarchical (\(\omega_{h}\)) and omega hierarchical subscale (\(\omega_{h-ss}\)). \(\omega_{h}\), represents the proportion of total-score variance due to a single, general construct that influences all items, despite the multidimensional nature of the item set (Flora, 2020a, 2020b). Our \(\omega_{h}\) value of 0.71 indicates that 71% of the variance of the GRMS total scores are attributable to individual differences on the general factor. \(\omega_{h-ss}\) for the subscales ranged from 0.21 to 0.43. Taken together, the omega values from our bifactor model suggest a strong general factor with subscales that are meaningful and useful.
11.14 Preparing an Overall APA Style Results Section
Model testing. To evaluate the models we, we used confirmatory factor analysis (CFA) in the R package, lavaan (v.0.6-17) with maximum likelihood estimation. Our sample size was 304. We selected fit criteria for their capacity to assess different aspects of the statistical analysis. As is common among SEM researchers, we reported the Chi-square goodness of fit (\(\chi^2\)). This evaluates the discrepancy between the unrestricted sample matrix and the restricted covariance matrix. Although the associated \(p\) value indicates adequate fit when the value is non-significant, it is widely recognized that large sample size can result in a statistically significant p value (Byrne, 2016a). The comparative fit index (CFI) is an incremental index, comparing the hypothesized model to the independent/baseline model. Adequate fit is determined when CFI values are at least .90 and perhaps higher than .95 (Kline, 2016). The root mean square error of approximation (RMSEA) takes into account the error of approximation in the population and expresses it per degree of freedom. As such, the fit indicator considers the complexity of the model. Ideal values are equal to or less than .05, values less than .08 represent reasonable fit, and values between .08 and .10 represent mediocre fit. The standardized root mean residual (SRMR) is a standardized measure of the mean absolute covariance residual – the overall difference between the observed and predicted correlations. Values greater than .10 may indicate poor fit and inspection of residuals is then advised. Because we were interested in comparing nested models we used the Chi-square difference test where a significant chi-square indicates statistically significant differences in models. Additionally, we used Akaike’s Information Criterion (AIC) and the Bayesian Information Criterion (BIC) that take model complexity and sample size into consideration. Models with lower values on each are considered to be superior. Kline (2016) advised researchers to be cautious when using these criteria as strict cut-offs. Elements such as sample size and model complexity should be considered when evaluating fit. Table 1 provides a side-by-side comparison of the resulting parameter estimates and fit statistics; Figures 1 and 2 provide a graphic representation of the models tested.
To assess the factor structure of the GRMSAAW we examined five separate models: a unidimensional model, an uncorrelated factors model, a correlated factors model, a second-order model, and a bifactor models. Support for a unidimensional model would suggest that the model is best represented by a total scale score with no subfactors. Support for an uncorrelated factors model would suggest that the factors are largely independent. Support for a correlated factors model would suggest that the factors are related. Support for a second-order GRMS factor would suggest that the AS, AF, MI, and AUA subfactors represent facets of the higher order factor, GRMS. In the bifactor models, items for each scale are loaded onto both their respective subscale and the overall GRMS scale (g). Support for this model would suggest that each subscale has both independent variance, and common variance that belongs to an underlying GRMS factor. When a bifactor model is the best representation of fit to the data, researchers can utilize bifactor indices to determine the proportion of variance accounted for by the subscales and the general factor, respectively.
Our first model was unidimensional where each of the 24 items loaded onto a single factor representing overall, gendered racial microaggressions towards Asian American women. The Chi-square index was statistically significant (\(\chi ^{2}(209) = 444.451, p < .001\)) indicating likely misfit. The CFI value of .81 indicated poor fit. In contrast, the RMSEA = 0.061, 90% CI(0.053, 0.069) and SRMR = 0.067 both fell within the ranges of acceptability. Our second model was an uncorrelated factors model. It demonstrated less than adequate fit to the data: \(\chi ^{2}(209) = 461.102, p < 0.001, CFI = 0.791, RMSEA = 0.063, 90%CI(0.055, 0.071), SRMR = 0.151\). Our third model was a single-order, correlated factors where each of the 22 items loaded onto one of four factors and the factors were free to correlate. The Chi-square index was not statistically signficant (\(\chi ^{2}(203)=232.453, p = 0.076\)) indicating reasonable fit. The CFI value of 0.972 exceeded the recommendation of .95. The RMSEA = 0.022 (90%CI[.000, 0.034]) was satisfactory. The SRMR value of 0.047 remained below the warning criteria of .10. Our fourth model represented a second order structure. Specifically, four first-order factors loaded onto a second factor model and demonstrated adequate fit to the data: \(\chi ^{2}(205) = 234.741, p = 0.076, CFI = 0.975, RMSEA = 0.022, 90%CI(0.000, 0.034), SRMR = .047\). The fifth model, a bifactor model regressed each item on its respective factor while simultaneously regressing each indicator onto an overall GRMS scale. This model had the best fit of those compared thus far: \(\chi ^{2}(187) = 164.080, p = .885, CFI = 0.997 , RMSEA = 0.009, 90%CI(0.000, 0.027, SRMR = 0.039\).
As shown in our table of model comparisons, Chi-square difference tests between models showed statistically significant differences between the uncorrelated factors model and the correlated factors and second-order model, which do not differ from each other. Finally, there was a statistically significant difference between the second order factor model and the bifactor model (\(\chi ^{2}(18) = 43.533, p < .001\)). The CFI, RMSEA, SRMR, and AIC values favor the bifactor model; the BIC favored the second order model. Thus, all of the multidimensional models demonstrated adequate fit and are suitable for research and practice.
As estimates of model-based internal consistency associated with the bifactor model, we calculated omega hierarchical (\(\omega_{h}\)) and omega hierarchical subscale (\(\omega_{h-ss}\)). \(\omega_{h}\), represents the proportion of total-score variance due to a single, general construct that influences all items, despite the multidimensional nature of the item set (Flora, 2020a, 2020b). Our \(\omega_{h}\) value of 0.71 indicated that 71% of the variance of the GRMS total scores are attributable to individual differences onthe general factor. \(\omega_{h-ss}\) for the subscales ranged from 0.21 to 0.43. Taken together, the omega values from our bifactor model suggest a strong general factor with subscales that are meaningful and useful.
11.15 A Conversation with Dr. Keum
Doctoral student Jadvir Gill (Industrial-Organizational Psychology) and I were able to interview the first author (Brian TaeHyuk Keum, PhD) about the article used for the research vignette (Keum et al., 2018). Here’s a direct link to that interview.
Among other things, we asked:
- What challenges did you encounter in the research process and recruiting participants?
- Can you describe how the items (or subscales) captures intersectional microaggressions for the intended population?
- How would you like to see the scale used in future science, practice, and advocacy?
- How are you using this scale in your current and future research?
11.16 Practice Problems
In each of these lessons I provide suggestions for practice that allow you to select one or more problems that are graded in difficulty. In psychometrics, I strongly recommend that you have started with a dataset that has a minimum of three subscales and use it for all of the assignments in the OER. The suggestion for practice spans the prior chapter and this one. For this combination assignment, you should plan to:
- Prepare the data frame for CFA.
- Specify and run unidimensional, single order (with correlated factors), second-order, and bifactor models.
- Narrate the adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR
- Write a mini-results section for each
- Compare model fit with \(\chi ^{2}\Delta\), AIC, and BIC.
- Calculate the appropriate omega reliability estimates for the g and specific factors.
- Write an APA style results sections with table(s) and figures.
11.16.1 Problem #1: Play around with this simulation.
The least complex is to change the random seed in the research and rework the problem demonstrated in the lesson. The results should map onto the ones obtained in the lecture.
11.16.2 Problem #2: Use simulated data from other lessons.
The second option involves utilizing one of the simulated datasets available in this OER. The last lesson in the OER contains three simulations that could be used for all of the statistics-based practice suggestions. Especially if you started with one of these examples in an earlier lesson, I highly recommend you continue with that.
Alternatively, Lewis and Neville’s (2015) Gendered Racial Microaggressions Scale for Black Women was used in the lessons for exploratory factor analysis and Conover et al.’s (2017) Ableist Microaggressions Scale is used in the lesson on invariance testing. Both of these would be suitable for the CFA homework assignments.
11.16.3 Problem #3: Try something entirely new.
As a third option, you are welcome to use data to which you have access and is suitable for CFA. This could include other simulated data, data found on an open access repository, data from the ReCentering Psych Stats survey described in the Qualtrics lesson, or your own data (presuming you have permission to use it).
11.16.4 Grading Rubric
Using the lecture and workflow (chart) as a guide, please work through all the steps listed in the proposed assignment/grading rubric.
| Assignment Component | Points Possible | Points Earned |
|---|---|---|
| 1. Prepare data for CFA (items only df, reverse-scored) | 5 | _____ |
| 2. Specify, run, and plot a unidimensional model | 5 | _____ |
| 3. Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section) | 5 | _____ |
| 4. Specify, run, and plot a single-order model with correlated factors | 5 | _____ |
| 5. Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section) | 5 | _____ |
| 6. Specify, run, and plot a second-order model | 5 | _____ |
| 7. Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section) | 5 | _____ |
| 8. Specify, run, and plot a bifactor model | 5 | _____ |
| 9. Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section) | 5 | _____ |
| 10. Compare model fit with \(\chi ^{2}\Delta\), AIC, BIC | 5 | _____ |
| 11. Calculate omega hierarchical (\(\omega_{h}\)) and omega-hierarchical-subscales (\(\omega_{h-ss}\)) | 5 | _____ |
| 12. APA style results with table(s) and figures | 5 | _____ |
| 13. Explanation to grader | 5 | _____ |
| Totals | 60 | _____ |
11.17 Homeworked Example
For more information about the data used in this homeworked example, please refer to the description and codebook located at the end of the introduction in first volume of ReCentering Psych Stats.
As a brief review, this data is part of an IRB-approved study, with consent to use in teaching demonstrations and to be made available to the general public via the open science framework. Hence, it is appropriate to use in this context. You will notice there are student- and teacher- IDs. These numbers are not actual student and teacher IDs, rather they were further re-identified so that they could not be connected to actual people.
Because this is an actual dataset, if you wish to work the problem along with me, you will need to download the ReC.rds data file from the Worked_Examples folder in the ReC_Psychometrics project on the GitHub.
The course evaluation items can be divided into three subscales:
- Valued by the student includes the items: ValObjectives, IncrUnderstanding, IncrInterest
- Traditional pedagogy includes the items: ClearResponsibilities, EffectiveAnswers, Feedback, ClearOrganization, ClearPresentation
- Socially responsive pedagogy includes the items: InclusvClassrm, EquitableEval, MultPerspectives, DEIintegration
In this Homeworked Example I will conduct all the analyses from the immediately prior (first order CFA models) and present CFA lessons. My hope is that the results will support my solution of three dimensions: valued-by-the-student, traditional pedagogy, socially responsive pedagogy. While the repetition of the prior lesson’s homeworked example is somewhat redundant, I am hopeful that this code will provide a fairly complete set of code for someone who is analyzing their own data from the beginning.
11.17.1 Prepare data for CFA (items only df, reverse-scored)
We can upload the data from the .rds file. The file should be in the same folder as the .rmd file. I’ve named the df object that holds the data “big.”
For the demonstration of CFA models, I will create an items-only df.
library(tidyverse)
items <- big %>%
dplyr::select(ValObjectives, IncrUnderstanding, IncrInterest, ClearResponsibilities,
EffectiveAnswers, Feedback, ClearOrganization, ClearPresentation,
MultPerspectives, InclusvClassrm, DEIintegration, EquitableEval)Let’s quickly check the structure. The variables should be numeric or integer.
Classes 'data.table' and 'data.frame': 310 obs. of 12 variables:
$ ValObjectives : int 5 5 4 4 5 5 5 5 4 5 ...
$ IncrUnderstanding : int 2 3 4 3 4 4 5 2 4 5 ...
$ IncrInterest : int 5 3 4 2 4 3 5 3 2 5 ...
$ ClearResponsibilities: int 5 5 4 4 5 4 5 4 4 5 ...
$ EffectiveAnswers : int 5 3 5 3 5 3 4 3 2 3 ...
$ Feedback : int 5 3 4 2 5 NA 5 4 4 5 ...
$ ClearOrganization : int 3 4 3 4 4 4 5 4 4 5 ...
$ ClearPresentation : int 4 4 4 2 5 3 4 4 4 5 ...
$ MultPerspectives : int 5 5 4 5 5 4 5 5 5 5 ...
$ InclusvClassrm : int 5 5 5 5 5 4 5 5 4 5 ...
$ DEIintegration : int 5 5 5 5 5 4 5 5 5 5 ...
$ EquitableEval : int 5 5 3 5 5 3 5 5 3 5 ...
- attr(*, ".internal.selfref")=<externalptr> 11.17.2 Specify and run a unidimensional model
First we map the relations we want to analyze.
uniD <- "CourseEvals =~ ValObjectives + IncrUnderstanding + IncrInterest + ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation + MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval"We analyze the relations by naming that object in our lavaan code.
set.seed(240311)
uniDfit <- lavaan::cfa(uniD, data = items)
lavaan::summary(uniDfit, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)lavaan 0.6.17 ended normally after 32 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Used Total
Number of observations 267 310
Model Test User Model:
Test statistic 344.973
Degrees of freedom 54
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 1940.157
Degrees of freedom 66
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.845
Tucker-Lewis Index (TLI) 0.810
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -3038.064
Loglikelihood unrestricted model (H1) -2865.578
Akaike (AIC) 6124.129
Bayesian (BIC) 6210.223
Sample-size adjusted Bayesian (SABIC) 6134.129
Root Mean Square Error of Approximation:
RMSEA 0.142
90 Percent confidence interval - lower 0.128
90 Percent confidence interval - upper 0.157
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.074
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
CourseEvals =~
ValObjectives 1.000 0.309 0.515
IncrUndrstndng 1.715 0.223 7.684 0.000 0.530 0.642
IncrInterest 2.142 0.269 7.971 0.000 0.662 0.685
ClearRspnsblts 2.065 0.239 8.652 0.000 0.638 0.808
EffectivAnswrs 2.105 0.244 8.617 0.000 0.650 0.800
Feedback 2.143 0.259 8.285 0.000 0.662 0.738
ClearOrganiztn 2.678 0.314 8.516 0.000 0.828 0.780
ClearPresenttn 2.521 0.285 8.832 0.000 0.779 0.846
MultPerspectvs 2.067 0.246 8.392 0.000 0.639 0.757
InclusvClassrm 1.246 0.170 7.324 0.000 0.385 0.592
DEIintegration 1.015 0.174 5.820 0.000 0.314 0.424
EquitableEval 1.435 0.179 8.027 0.000 0.443 0.694
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ValObjectives 0.265 0.024 11.254 0.000 0.265 0.735
.IncrUndrstndng 0.401 0.037 10.970 0.000 0.401 0.588
.IncrInterest 0.494 0.046 10.815 0.000 0.494 0.530
.ClearRspnsblts 0.217 0.022 9.983 0.000 0.217 0.348
.EffectivAnswrs 0.237 0.024 10.060 0.000 0.237 0.359
.Feedback 0.367 0.035 10.555 0.000 0.367 0.455
.ClearOrganiztn 0.439 0.043 10.250 0.000 0.439 0.391
.ClearPresenttn 0.242 0.026 9.446 0.000 0.242 0.285
.MultPerspectvs 0.304 0.029 10.431 0.000 0.304 0.427
.InclusvClassrm 0.275 0.025 11.104 0.000 0.275 0.649
.DEIintegration 0.449 0.040 11.372 0.000 0.449 0.820
.EquitableEval 0.211 0.020 10.777 0.000 0.211 0.518
CourseEvals 0.096 0.022 4.381 0.000 1.000 1.000
R-Square:
Estimate
ValObjectives 0.265
IncrUndrstndng 0.412
IncrInterest 0.470
ClearRspnsblts 0.652
EffectivAnswrs 0.641
Feedback 0.545
ClearOrganiztn 0.609
ClearPresenttn 0.715
MultPerspectvs 0.573
InclusvClassrm 0.351
DEIintegration 0.180
EquitableEval 0.482Let’s plot the results to see if the figure resembles what we intended to specify.
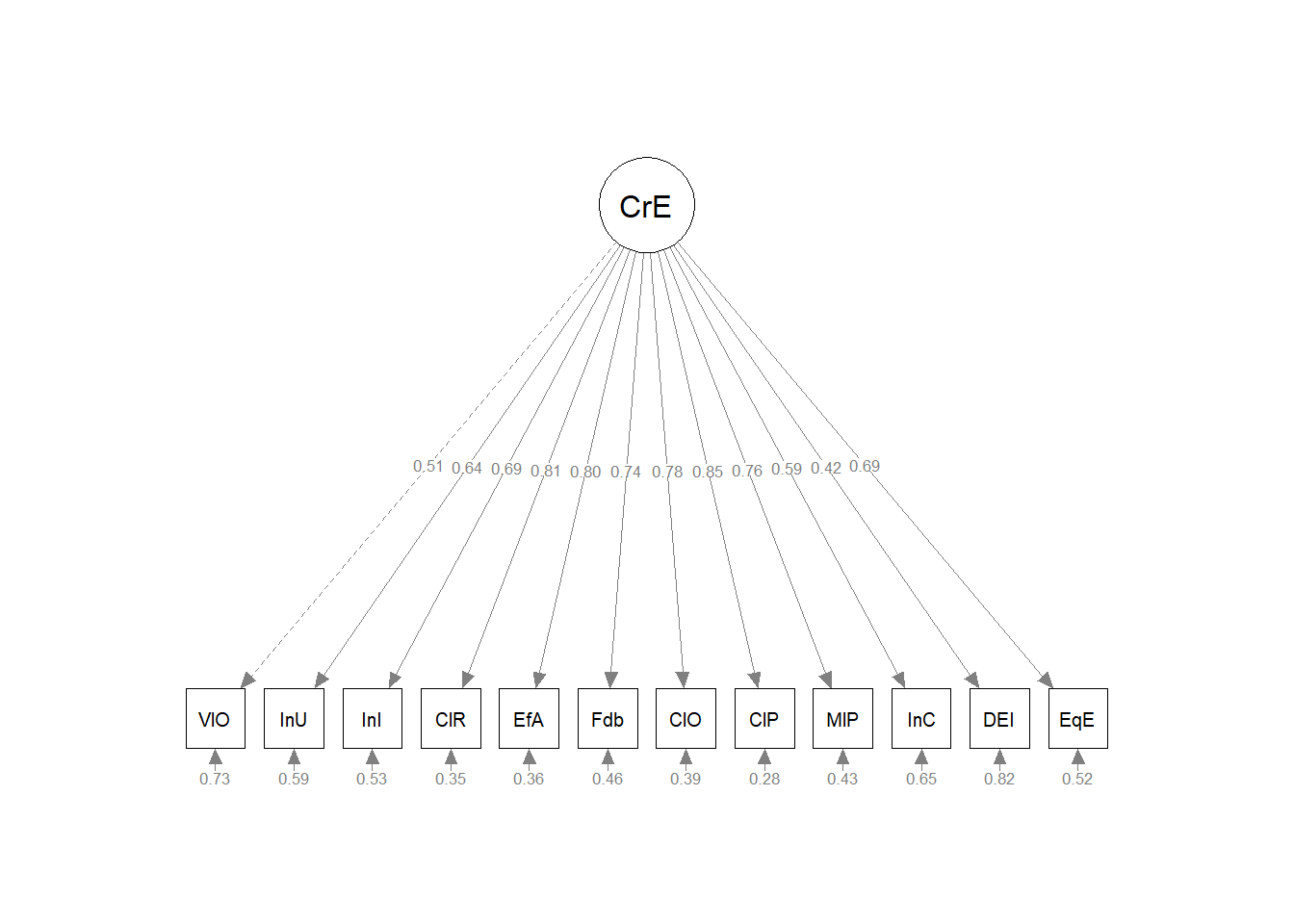
11.17.3 Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section)
Model testing. To evaluate the models we, we used confirmatory factor analysis (CFA) in the R package, lavaan (v.0-6.17) with maximum likelihood estimation. Our sample size was 267 We selected fit criteria for their capacity to assess different aspects of the statistical analysis. As is common among SEM researchers, we reported the Chi-square goodness of fit (χ2). This evaluates the discrepancy between the unrestricted sample matrix and the restricted covariance matrix. Although the associated p-value indicates adequate fit when the value is non-significant, it is widely recognized that a large sample size can result in a statistically significant p value (Byrne, 2016b). The comparative fit index (CFI) is an incremental index, comparing the hypothesized model to the independent/baseline model. Adequate fit is determined when CFI values are at least .90 and perhaps higher than .95 (Kline, 2016). The root mean square error of approximation (RMSEA) takes into account the error of approximation in the population and expresses it per degree of freedom. As such, the fit indicator considers the complexity of the model. Ideal values are equal to or less than .05, values less than .08 represent reasonable fit, and values between .08 and .10 represent mediocre fit. The standardized root mean residual (SRMR) is a standardized measure of the mean absolute covariance residual – the overall difference between the observed and predicted correlations. Values greater than .10 may indicate poor fit and inspection of residuals is then advised. Kline (2016) advised researchers to be cautious when using these criteria as strict cut-offs. Elements such as sample size and model complexity should be considered when evaluating fit.
Our first model was unidimensional where each of the 12 items loaded onto a single factor representing overall course evaluations. The Chi-square index was statistically significant \((\chi^2(54)=344.97, p<.001)\) indicating likely misfit. The CFI value of .85 indicated poor fit. The RMSEA = .14 (90% CI [.13, .16]) suggested serious problems. The SRMR value of .07 was below the warning criteria of .10. The AIC and BIC values were 6124.13 and 6134.13, respectively, and will become useful in comparing subsequent models.
11.17.5 Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section)
Our second model was a single-order, multidimensional model where each of the 12 items loaded onto one of four factors. Standardized pattern coefficients ranged between .74 and .85 on the TradPed factor, between .56 and .84 on the Valued factor, and between .57 and .85 on the SCRPed factor. The Chi-square index was statistically significant \((\chi^2(51) = 224.795, p < 0.001\) indicating some degree of misfit. The CFI value of .91 fell below the recommendation of .95. The RMSEA = .113 (90% CI [.098, .128]) was higher than recommended. The SRMR value of .061 remained below the warning criteria of .10. The AIC and BIC values were 6009.95 and 6021.20, respectively.
11.17.6 Specify and run a second-order model
secondM <- "TradPed =~ ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation
Valued =~ ValObjectives + IncrUnderstanding + IncrInterest
SCRPed =~ MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval
Evals =~ TradPed + Valued + SCRPed"set.seed(240311)
secondF <- lavaan::cfa(secondM, data = items)
lavaan::summary(secondF, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)lavaan 0.6.17 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 27
Used Total
Number of observations 267 310
Model Test User Model:
Test statistic 224.795
Degrees of freedom 51
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 1940.157
Degrees of freedom 66
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.907
Tucker-Lewis Index (TLI) 0.880
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -2977.975
Loglikelihood unrestricted model (H1) -2865.578
Akaike (AIC) 6009.951
Bayesian (BIC) 6106.807
Sample-size adjusted Bayesian (SABIC) 6021.201
Root Mean Square Error of Approximation:
RMSEA 0.113
90 Percent confidence interval - lower 0.098
90 Percent confidence interval - upper 0.128
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.061
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
TradPed =~
ClearRspnsblts 1.000 0.652 0.826
EffectivAnswrs 1.015 0.065 15.606 0.000 0.662 0.815
Feedback 1.010 0.075 13.481 0.000 0.659 0.735
ClearOrganiztn 1.295 0.086 15.106 0.000 0.845 0.797
ClearPresenttn 1.204 0.072 16.680 0.000 0.785 0.853
Valued =~
ValObjectives 1.000 0.334 0.557
IncrUndrstndng 1.942 0.223 8.717 0.000 0.649 0.786
IncrInterest 2.438 0.273 8.932 0.000 0.815 0.844
SCRPed =~
MultPerspectvs 1.000 0.713 0.846
InclusvClassrm 0.622 0.053 11.672 0.000 0.444 0.682
DEIintegration 0.589 0.063 9.365 0.000 0.420 0.567
EquitableEval 0.642 0.052 12.410 0.000 0.458 0.717
Evals =~
TradPed 1.000 0.980 0.980
Valued 0.419 0.055 7.630 0.000 0.801 0.801
SCRPed 0.958 0.086 11.128 0.000 0.859 0.859
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ClearRspnsblts 0.199 0.021 9.456 0.000 0.199 0.319
.EffectivAnswrs 0.222 0.023 9.618 0.000 0.222 0.336
.Feedback 0.371 0.036 10.415 0.000 0.371 0.460
.ClearOrganiztn 0.410 0.042 9.855 0.000 0.410 0.365
.ClearPresenttn 0.232 0.026 8.939 0.000 0.232 0.273
.ValObjectives 0.248 0.023 10.650 0.000 0.248 0.690
.IncrUndrstndng 0.260 0.032 8.041 0.000 0.260 0.382
.IncrInterest 0.268 0.043 6.308 0.000 0.268 0.288
.MultPerspectvs 0.203 0.029 7.052 0.000 0.203 0.285
.InclusvClassrm 0.226 0.023 10.028 0.000 0.226 0.534
.DEIintegration 0.371 0.035 10.734 0.000 0.371 0.678
.EquitableEval 0.198 0.020 9.685 0.000 0.198 0.486
.TradPed 0.017 0.023 0.728 0.467 0.039 0.039
.Valued 0.040 0.010 3.895 0.000 0.358 0.358
.SCRPed 0.134 0.032 4.219 0.000 0.263 0.263
Evals 0.409 0.056 7.281 0.000 1.000 1.000
R-Square:
Estimate
ClearRspnsblts 0.681
EffectivAnswrs 0.664
Feedback 0.540
ClearOrganiztn 0.635
ClearPresenttn 0.727
ValObjectives 0.310
IncrUndrstndng 0.618
IncrInterest 0.712
MultPerspectvs 0.715
InclusvClassrm 0.466
DEIintegration 0.322
EquitableEval 0.514
TradPed 0.961
Valued 0.642
SCRPed 0.737As we plot this model we expect to see a “second level” factor predicting each of the “first order” factors. The indicator was set on GRM –> AS. Each of the four factors predicts only the items associated with their factor with one item for each factor (the first on the left) specified as the indicator variable.
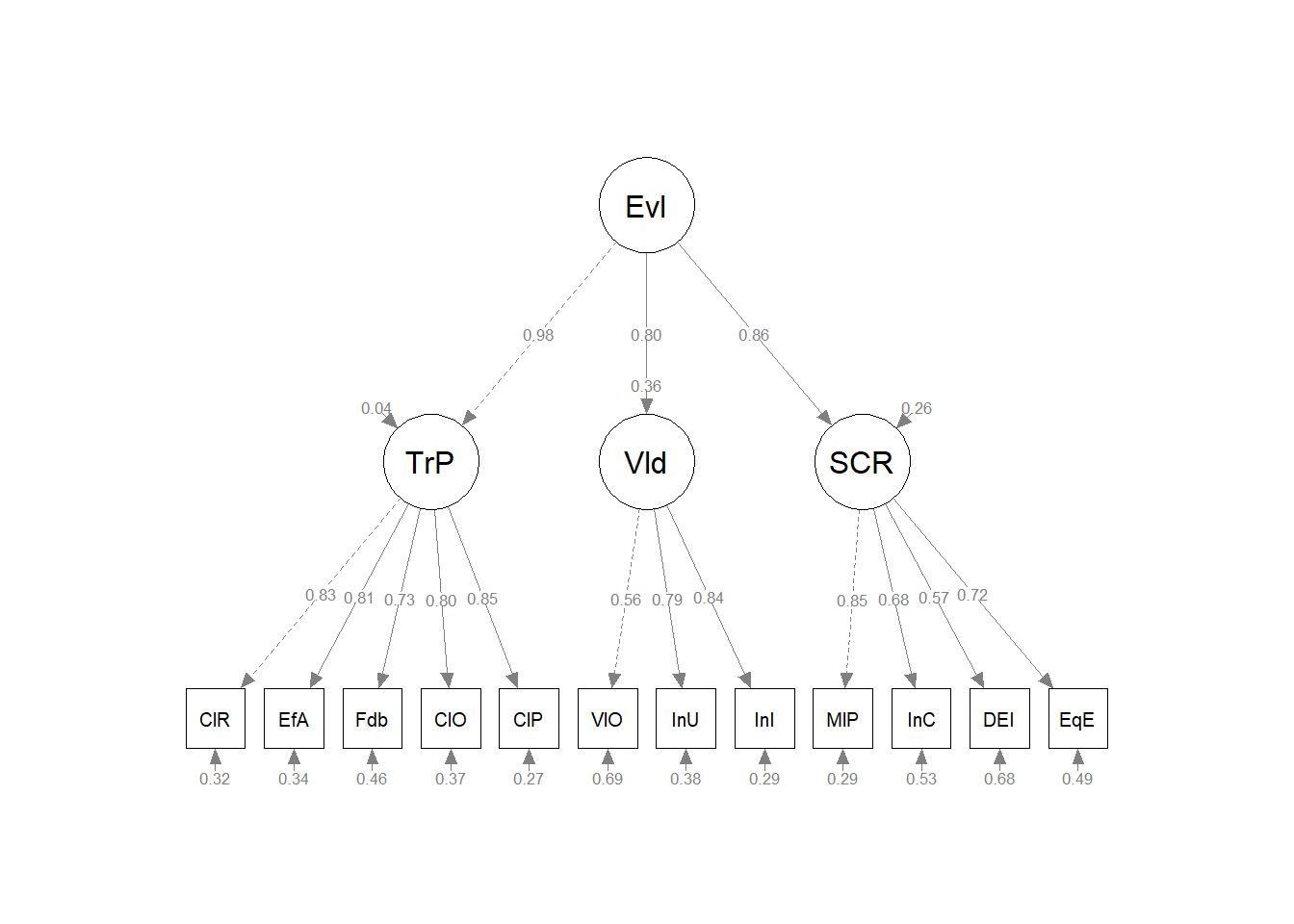 Code for saving the results as a .csv file.
Code for saving the results as a .csv file.
secondFFitStats <- tidySEM::table_fit(secondF)
secondF_paramEsts <- tidySEM::table_results(secondF, digits = 3, columns = NULL)
# In a second order structure there are no correlations to request
# secondFCorrs <- tidySEM::table_cors(secondF, digits=3)
# to see each of the tables, remove the hashtab secondFFitStats
# secondF_paramEstsNext, I export them.
11.17.7 Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section)
Our next model represented a second order structure where three first-order factors loaded onto a second factor model. Across a variety of indices, model fit improved: \(\chi^{2}(51) = 224.80, p < .001, CFI = .907, RMSEA = .113, 90%CI(.098, .128), SRMR = .061\). Factor loadings ranged from .75 to .85 for the TradPed scale, .56 to .84 for the Valued-by-Me scale, .57 to .85 for the SCRPed scale, and .80 to .98 for the total scale.
11.17.8 Specify and run a bifactor model
bifacM <- "Evals =~ ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation + ValObjectives + IncrUnderstanding + IncrInterest + MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval
TradPed =~ ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation
Valued =~ ValObjectives + IncrUnderstanding + IncrInterest
SCRPed =~ MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval
#fixes the relations between g and each of the factors to 0.0
Evals ~~ 0*TradPed
Evals ~~ 0*Valued
Evals ~~ 0*SCRPed
#fixes the relations (covariances) between each of the factors to 0.0
TradPed ~~ 0*Valued
TradPed ~~ 0*SCRPed
Valued ~~ 0*SCRPed
"Warning in lavaan::lavaan(model = bifacM, data = items, int.ov.free = TRUE, : lavaan WARNING:
the optimizer (NLMINB) claimed the model converged, but not all
elements of the gradient are (near) zero; the optimizer may not
have found a local solution use check.gradient = FALSE to skip
this check.Warning in lav_object_summary(object = object, header = header, fit.measures = fit.measures, : lavaan WARNING: fit measures not available if model did not convergelavaan 0.6.17 did NOT end normally after 1256 iterations
** WARNING ** Estimates below are most likely unreliable
Estimator ML
Optimization method NLMINB
Number of model parameters 36
Used Total
Number of observations 267 310
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals =~
ClearRspnsblts 1.000 0.665 0.842
EffectivAnswrs 0.977 NA 0.650 0.800
Feedback 1.032 NA 0.686 0.765
ClearOrganiztn 1.251 NA 0.832 0.785
ClearPresenttn 1.227 NA 0.816 0.886
ValObjectives 0.436 NA 0.290 0.484
IncrUndrstndng 0.757 NA 0.504 0.610
IncrInterest 0.923 NA 0.614 0.636
MultPerspectvs 0.925 NA 0.615 0.730
InclusvClassrm 0.531 NA 0.353 0.543
DEIintegration 0.387 NA 0.258 0.348
EquitableEval 0.644 NA 0.429 0.671
TradPed =~
ClearRspnsblts 1.000 0.018 0.023
EffectivAnswrs -0.115 NA -0.002 -0.003
Feedback 2.260 NA 0.040 0.045
ClearOrganiztn -0.130 NA -0.002 -0.002
ClearPresenttn -146.233 NA -2.614 -2.838
Valued =~
ValObjectives 1.000 0.145 0.241
IncrUndrstndng 2.548 NA 0.368 0.446
IncrInterest 4.310 NA 0.623 0.645
SCRPed =~
MultPerspectvs 1.000 0.267 0.316
InclusvClassrm 1.302 NA 0.347 0.534
DEIintegration 2.188 NA 0.584 0.788
EquitableEval 0.415 NA 0.111 0.173
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals ~~
TradPed 0.000 0.000 0.000
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
TradPed ~~
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
Valued ~~
SCRPed 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ClearRspnsblts 0.182 NA 0.182 0.291
.EffectivAnswrs 0.238 NA 0.238 0.361
.Feedback 0.332 NA 0.332 0.413
.ClearOrganiztn 0.432 NA 0.432 0.384
.ClearPresenttn -6.651 NA -6.651 -7.837
.ValObjectives 0.255 NA 0.255 0.708
.IncrUndrstndng 0.292 NA 0.292 0.429
.IncrInterest 0.167 NA 0.167 0.179
.MultPerspectvs 0.262 NA 0.262 0.368
.InclusvClassrm 0.178 NA 0.178 0.421
.DEIintegration 0.141 NA 0.141 0.257
.EquitableEval 0.212 NA 0.212 0.519
Evals 0.443 NA 1.000 1.000
TradPed 0.000 NA 1.000 1.000
Valued 0.021 NA 1.000 1.000
SCRPed 0.071 NA 1.000 1.000
R-Square:
Estimate
ClearRspnsblts 0.709
EffectivAnswrs 0.639
Feedback 0.587
ClearOrganiztn 0.616
ClearPresenttn NA
ValObjectives 0.292
IncrUndrstndng 0.571
IncrInterest 0.821
MultPerspectvs 0.632
InclusvClassrm 0.579
DEIintegration 0.743
EquitableEval 0.481Unfortunately, it’s all-too-common for complex models to fail to converge. When this happens it’s a slow, tedious process to find a fix.
In the ReCentering Psych Stats example I was able to fix it by adding a check.gradient=FALSE statement. So, let’s try that
Warning in lav_model_vcov(lavmodel = lavmodel, lavsamplestats = lavsamplestats, : lavaan WARNING:
Could not compute standard errors! The information matrix could
not be inverted. This may be a symptom that the model is not
identified.Warning in lav_object_post_check(object): lavaan WARNING: some estimated ov
variances are negativelavaan 0.6.17 ended normally after 1256 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 36
Used Total
Number of observations 267 310
Model Test User Model:
Test statistic 121.965
Degrees of freedom 42
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 1940.157
Degrees of freedom 66
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.957
Tucker-Lewis Index (TLI) 0.933
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -2926.561
Loglikelihood unrestricted model (H1) -2865.578
Akaike (AIC) 5925.121
Bayesian (BIC) 6054.262
Sample-size adjusted Bayesian (SABIC) 5940.121
Root Mean Square Error of Approximation:
RMSEA 0.084
90 Percent confidence interval - lower 0.067
90 Percent confidence interval - upper 0.102
P-value H_0: RMSEA <= 0.050 0.001
P-value H_0: RMSEA >= 0.080 0.679
Standardized Root Mean Square Residual:
SRMR 0.041
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals =~
ClearRspnsblts 1.000 0.665 0.842
EffectivAnswrs 0.977 NA 0.650 0.800
Feedback 1.032 NA 0.686 0.765
ClearOrganiztn 1.251 NA 0.832 0.785
ClearPresenttn 1.227 NA 0.816 0.886
ValObjectives 0.436 NA 0.290 0.484
IncrUndrstndng 0.757 NA 0.504 0.610
IncrInterest 0.923 NA 0.614 0.636
MultPerspectvs 0.925 NA 0.615 0.730
InclusvClassrm 0.531 NA 0.353 0.543
DEIintegration 0.387 NA 0.258 0.348
EquitableEval 0.644 NA 0.429 0.671
TradPed =~
ClearRspnsblts 1.000 0.018 0.023
EffectivAnswrs -0.115 NA -0.002 -0.003
Feedback 2.260 NA 0.040 0.045
ClearOrganiztn -0.130 NA -0.002 -0.002
ClearPresenttn -146.233 NA -2.614 -2.838
Valued =~
ValObjectives 1.000 0.145 0.241
IncrUndrstndng 2.548 NA 0.368 0.446
IncrInterest 4.310 NA 0.623 0.645
SCRPed =~
MultPerspectvs 1.000 0.267 0.316
InclusvClassrm 1.302 NA 0.347 0.534
DEIintegration 2.188 NA 0.584 0.788
EquitableEval 0.415 NA 0.111 0.173
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals ~~
TradPed 0.000 0.000 0.000
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
TradPed ~~
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
Valued ~~
SCRPed 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ClearRspnsblts 0.182 NA 0.182 0.291
.EffectivAnswrs 0.238 NA 0.238 0.361
.Feedback 0.332 NA 0.332 0.413
.ClearOrganiztn 0.432 NA 0.432 0.384
.ClearPresenttn -6.651 NA -6.651 -7.837
.ValObjectives 0.255 NA 0.255 0.708
.IncrUndrstndng 0.292 NA 0.292 0.429
.IncrInterest 0.167 NA 0.167 0.179
.MultPerspectvs 0.262 NA 0.262 0.368
.InclusvClassrm 0.178 NA 0.178 0.421
.DEIintegration 0.141 NA 0.141 0.257
.EquitableEval 0.212 NA 0.212 0.519
Evals 0.443 NA 1.000 1.000
TradPed 0.000 NA 1.000 1.000
Valued 0.021 NA 1.000 1.000
SCRPed 0.071 NA 1.000 1.000
R-Square:
Estimate
ClearRspnsblts 0.709
EffectivAnswrs 0.639
Feedback 0.587
ClearOrganiztn 0.616
ClearPresenttn NA
ValObjectives 0.292
IncrUndrstndng 0.571
IncrInterest 0.821
MultPerspectvs 0.632
InclusvClassrm 0.579
DEIintegration 0.743
EquitableEval 0.481That did not work.
I found an article on nonconvergence in bifactor models: https://stackoverflow.com/questions/68837355/trouble-converging-bifactor-model-using-lavaan
I took out the check.gradient command and swapped in the “std.lv=TRUE” command.
Warning in lav_object_post_check(object): lavaan WARNING: some estimated ov
variances are negativelavaan 0.6.17 ended normally after 521 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 36
Used Total
Number of observations 267 310
Model Test User Model:
Test statistic 121.965
Degrees of freedom 42
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 1940.157
Degrees of freedom 66
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.957
Tucker-Lewis Index (TLI) 0.933
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -2926.561
Loglikelihood unrestricted model (H1) -2865.578
Akaike (AIC) 5925.121
Bayesian (BIC) 6054.262
Sample-size adjusted Bayesian (SABIC) 5940.121
Root Mean Square Error of Approximation:
RMSEA 0.084
90 Percent confidence interval - lower 0.067
90 Percent confidence interval - upper 0.102
P-value H_0: RMSEA <= 0.050 0.001
P-value H_0: RMSEA >= 0.080 0.679
Standardized Root Mean Square Residual:
SRMR 0.041
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals =~
ClearRspnsblts 0.665 0.040 16.440 0.000 0.665 0.842
EffectivAnswrs 0.650 0.043 15.284 0.000 0.650 0.800
Feedback 0.686 0.048 14.204 0.000 0.686 0.765
ClearOrganiztn 0.832 0.056 14.873 0.000 0.832 0.785
ClearPresenttn 0.816 0.048 17.021 0.000 0.816 0.886
ValObjectives 0.290 0.035 8.203 0.000 0.290 0.484
IncrUndrstndng 0.504 0.047 10.784 0.000 0.504 0.610
IncrInterest 0.614 0.054 11.355 0.000 0.614 0.636
MultPerspectvs 0.615 0.045 13.572 0.000 0.615 0.730
InclusvClassrm 0.353 0.038 9.350 0.000 0.353 0.543
DEIintegration 0.258 0.045 5.718 0.000 0.258 0.348
EquitableEval 0.429 0.035 12.164 0.000 0.429 0.671
TradPed =~
ClearRspnsblts -0.018 0.234 -0.076 0.940 -0.018 -0.022
EffectivAnswrs 0.002 0.028 0.073 0.942 0.002 0.002
Feedback -0.040 0.529 -0.076 0.940 -0.040 -0.045
ClearOrganiztn 0.002 0.032 0.072 0.943 0.002 0.002
ClearPresenttn 2.637 34.860 0.076 0.940 2.637 2.863
Valued =~
ValObjectives 0.145 0.042 3.472 0.001 0.145 0.241
IncrUndrstndng 0.368 0.076 4.878 0.000 0.368 0.446
IncrInterest 0.623 0.116 5.385 0.000 0.623 0.645
SCRPed =~
MultPerspectvs 0.267 0.042 6.327 0.000 0.267 0.316
InclusvClassrm 0.347 0.042 8.251 0.000 0.347 0.534
DEIintegration 0.584 0.059 9.967 0.000 0.584 0.788
EquitableEval 0.111 0.034 3.224 0.001 0.111 0.173
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals ~~
TradPed 0.000 0.000 0.000
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
TradPed ~~
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
Valued ~~
SCRPed 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ClearRspnsblts 0.182 0.021 8.669 0.000 0.182 0.291
.EffectivAnswrs 0.238 0.025 9.441 0.000 0.238 0.361
.Feedback 0.333 0.047 7.050 0.000 0.333 0.413
.ClearOrganiztn 0.432 0.045 9.663 0.000 0.432 0.384
.ClearPresenttn -6.774 183.878 -0.037 0.971 -6.774 -7.982
.ValObjectives 0.255 0.023 10.940 0.000 0.255 0.708
.IncrUndrstndng 0.292 0.054 5.440 0.000 0.292 0.429
.IncrInterest 0.167 0.137 1.221 0.222 0.167 0.179
.MultPerspectvs 0.262 0.026 9.965 0.000 0.262 0.368
.InclusvClassrm 0.178 0.024 7.298 0.000 0.178 0.421
.DEIintegration 0.141 0.056 2.496 0.013 0.141 0.257
.EquitableEval 0.212 0.019 10.967 0.000 0.212 0.519
Evals 1.000 1.000 1.000
TradPed 1.000 1.000 1.000
Valued 1.000 1.000 1.000
SCRPed 1.000 1.000 1.000
R-Square:
Estimate
ClearRspnsblts 0.709
EffectivAnswrs 0.639
Feedback 0.587
ClearOrganiztn 0.616
ClearPresenttn NA
ValObjectives 0.292
IncrUndrstndng 0.571
IncrInterest 0.821
MultPerspectvs 0.632
InclusvClassrm 0.579
DEIintegration 0.743
EquitableEval 0.481Great! It ran, but now I have negative variances (i.e., a “Heywood case”) so I need to fix that. In the “variances” you can see the negative values on: .ClearPresenttn
Here’s an article about Heywood cases (i.e., where there are negative variances): https://s3.amazonaws.com/assets.datacamp.com/production/course_6419/slides/chapter3.pdf
[1] 0.8518206I will add this statement:
ClearPresentation~~0.852*ClearPresentation
bifacM <- "Evals =~ ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation + ValObjectives + IncrUnderstanding + IncrInterest + MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval
TradPed =~ ClearResponsibilities + EffectiveAnswers + Feedback + ClearOrganization + ClearPresentation
Valued =~ ValObjectives + IncrUnderstanding + IncrInterest
SCRPed =~ MultPerspectives + InclusvClassrm + DEIintegration + EquitableEval
ClearPresentation~~0.852*ClearPresentation
#fixes the relations between g and each of the factors to 0.0
Evals ~~ 0*TradPed
Evals ~~ 0*Valued
Evals ~~ 0*SCRPed
#fixes the relations (covariances) between each of the factors to 0.0
TradPed ~~ 0*Valued
TradPed ~~ 0*SCRPed
Valued ~~ 0*SCRPed
"set.seed(240311)
bifacF <- lavaan::cfa(bifacM, data = items, std.lv = TRUE)
lavaan::summary(bifacF, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)lavaan 0.6.17 ended normally after 48 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 35
Number of observations 267
Model Test User Model:
Test statistic 262.623
Degrees of freedom 43
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 1940.157
Degrees of freedom 66
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.883
Tucker-Lewis Index (TLI) 0.820
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -2996.890
Loglikelihood unrestricted model (H1) -2865.578
Akaike (AIC) 6063.779
Bayesian (BIC) 6189.333
Sample-size adjusted Bayesian (SABIC) 6078.362
Root Mean Square Error of Approximation:
RMSEA 0.138
90 Percent confidence interval - lower 0.122
90 Percent confidence interval - upper 0.155
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.084
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals =~
ClearRspnsblts 0.621 0.045 13.943 0.000 0.621 0.786
EffectivAnswrs 0.637 0.045 14.110 0.000 0.637 0.784
Feedback 0.679 0.050 13.532 0.000 0.679 0.756
ClearOrganiztn 0.798 0.061 13.135 0.000 0.798 0.753
ClearPresenttn 0.721 0.070 10.301 0.000 0.721 0.613
ValObjectives 0.293 0.037 7.996 0.000 0.293 0.488
IncrUndrstndng 0.496 0.048 10.227 0.000 0.496 0.600
IncrInterest 0.638 0.055 11.557 0.000 0.638 0.661
MultPerspectvs 0.643 0.046 13.886 0.000 0.643 0.763
InclusvClassrm 0.359 0.040 9.079 0.000 0.359 0.552
DEIintegration 0.286 0.047 6.062 0.000 0.286 0.386
EquitableEval 0.455 0.036 12.710 0.000 0.455 0.713
TradPed =~
ClearRspnsblts 0.394 0.170 2.313 0.021 0.394 0.498
EffectivAnswrs 0.121 0.086 1.405 0.160 0.121 0.149
Feedback 0.085 0.081 1.050 0.294 0.085 0.095
ClearOrganiztn 0.215 0.136 1.582 0.114 0.215 0.203
ClearPresenttn 0.118 0.112 1.052 0.293 0.118 0.100
Valued =~
ValObjectives 0.141 0.043 3.248 0.001 0.141 0.235
IncrUndrstndng 0.385 0.081 4.752 0.000 0.385 0.466
IncrInterest 0.578 0.111 5.188 0.000 0.578 0.598
SCRPed =~
MultPerspectvs 0.226 0.047 4.824 0.000 0.226 0.268
InclusvClassrm 0.335 0.051 6.577 0.000 0.335 0.515
DEIintegration 0.574 0.073 7.859 0.000 0.574 0.775
EquitableEval 0.073 0.036 2.002 0.045 0.073 0.114
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
Evals ~~
TradPed 0.000 0.000 0.000
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
TradPed ~~
Valued 0.000 0.000 0.000
SCRPed 0.000 0.000 0.000
Valued ~~
SCRPed 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.ClearPresenttn 0.852 0.852 0.615
.ClearRspnsblts 0.084 0.134 0.627 0.530 0.084 0.135
.EffectivAnswrs 0.240 0.025 9.637 0.000 0.240 0.363
.Feedback 0.337 0.034 9.812 0.000 0.337 0.419
.ClearOrganiztn 0.440 0.050 8.847 0.000 0.440 0.392
.ValObjectives 0.255 0.023 10.921 0.000 0.255 0.707
.IncrUndrstndng 0.288 0.058 4.942 0.000 0.288 0.422
.IncrInterest 0.191 0.120 1.598 0.110 0.191 0.205
.MultPerspectvs 0.247 0.027 9.281 0.000 0.247 0.347
.InclusvClassrm 0.182 0.028 6.557 0.000 0.182 0.430
.DEIintegration 0.137 0.074 1.849 0.064 0.137 0.250
.EquitableEval 0.195 0.019 10.102 0.000 0.195 0.479
Evals 1.000 1.000 1.000
TradPed 1.000 1.000 1.000
Valued 1.000 1.000 1.000
SCRPed 1.000 1.000 1.000
R-Square:
Estimate
ClearPresenttn 0.385
ClearRspnsblts 0.865
EffectivAnswrs 0.637
Feedback 0.581
ClearOrganiztn 0.608
ValObjectives 0.293
IncrUndrstndng 0.578
IncrInterest 0.795
MultPerspectvs 0.653
InclusvClassrm 0.570
DEIintegration 0.750
EquitableEval 0.521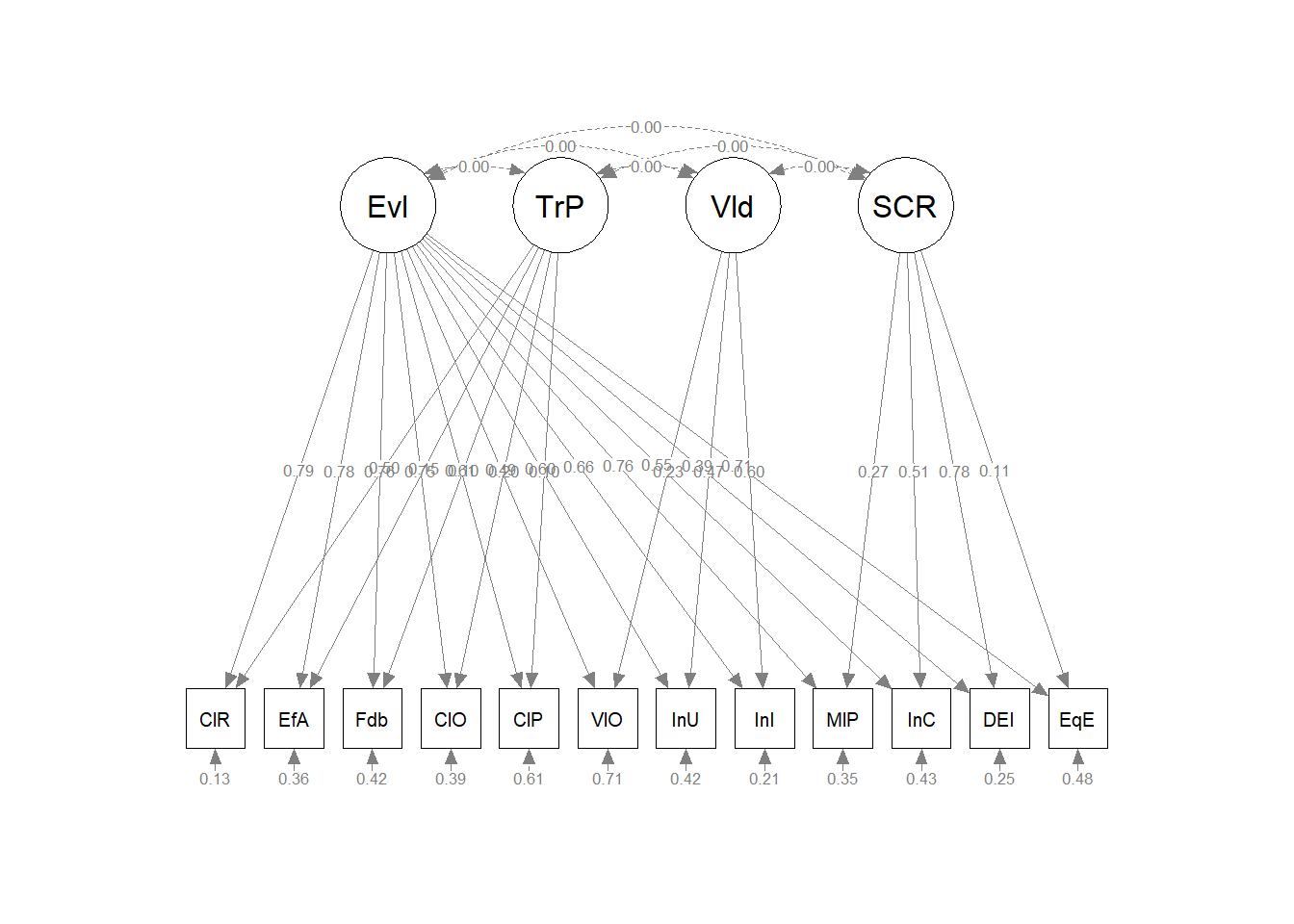 In making our map the first 12 values refer to the items, 13 refers to g, and 14-16 point to the factors.
In making our map the first 12 values refer to the items, 13 refers to g, and 14-16 point to the factors.
m = matrix(nrow = 3, ncol = 12)
m[1, ] = c(14, 0, 0, 0, 0, 15, 0, 0, 0, 0, 0, 16)
m[2, ] = 1:12
m[3, ] = c(0, 0, 0, 0, 0, 13, 0, 0, 0, 0, 0, 0)
m [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
[1,] 14 0 0 0 0 15 0 0 0 0 0 16
[2,] 1 2 3 4 5 6 7 8 9 10 11 12
[3,] 0 0 0 0 0 13 0 0 0 0 0 0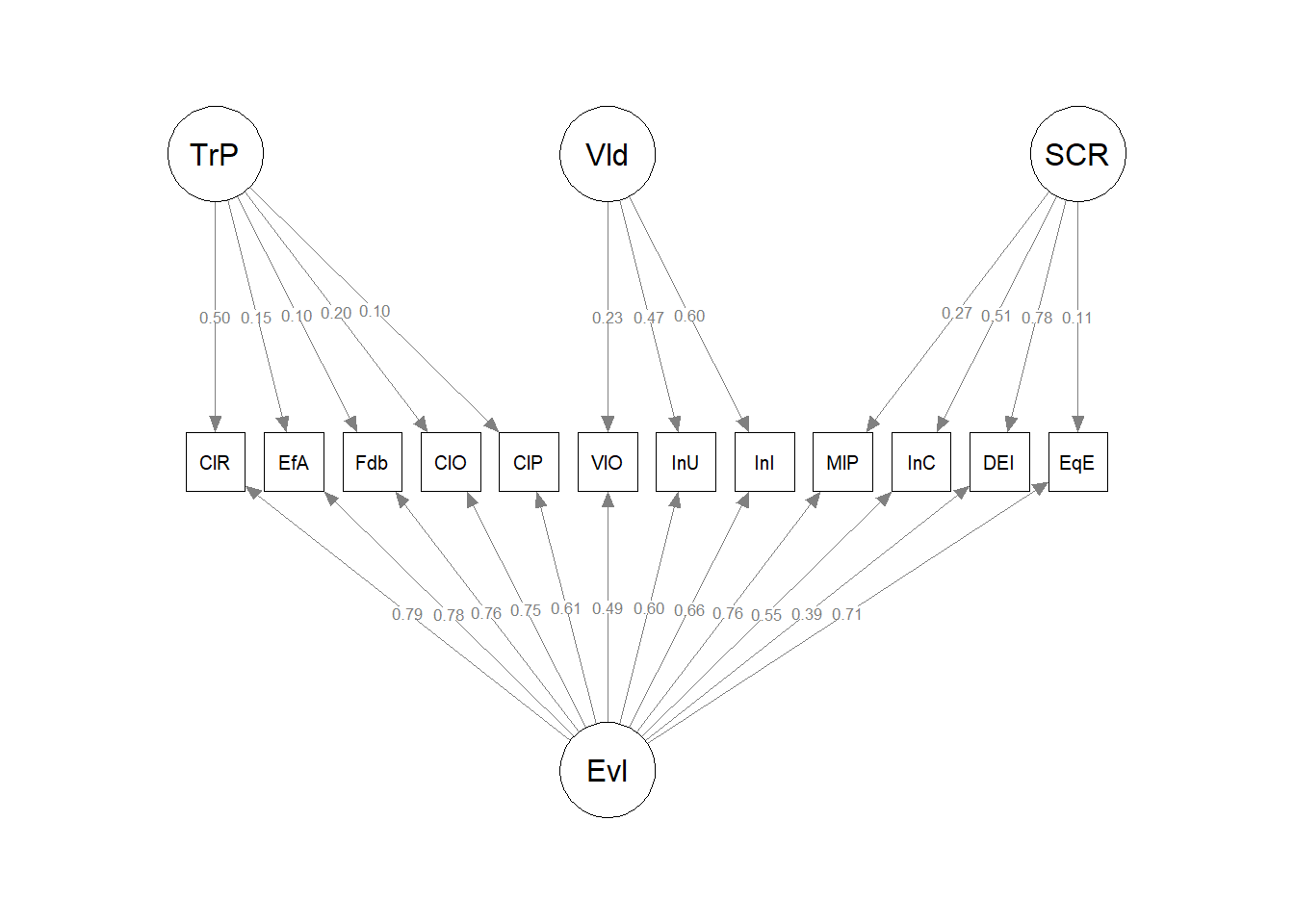 Code for saving the results as a .csv file.
Code for saving the results as a .csv file.
bifacFFitStats <- tidySEM::table_fit(bifacF)
bifacF_paramEsts <- tidySEM::table_results(bifacF, digits = 3, columns = NULL)
bifacFCorrs <- tidySEM::table_cors(bifacF, digits = 3)
# to see each of the tables, remove the hashtab corrFitStats
# corrF_paramEsts corrFCorrsNext, I export them.
11.17.9 Narrate adequacy of fit with \(\chi ^{2}\), CFI, RMSEA, SRMR (write a mini-results section)
The bifactor model regressed each item on its respective factor while simultaneously regressing each indicator onto an overall evaluation scale. The initial specification failed to converge. Adding the “std.lv = TRUE” to the lavaan::cfa function resulted in convergence. It also identified a negative covariance (i.e., a “Heywood” case). We resolved this issue by respecifying the model with a multiplication of the variance of the item (ClearPresentation) onto itself. This model had the second best fit of those compared thus far: \(\chi^2(43)=262.62, p < .001, CFI = .883, RMSEA = .138, 90%CI [.122, .155], SRMR = .084\) (the correlated factors and second order structures had the best fit). Factor loadings for the three factors ranged from .10 to .50 for the TradPed scale, .24 to .60 for the Valued-by-me scale, and .11 to .78 for the SCRPed scale. Factor loadings for the overall evaluation scale (g) ranged from .37 to .79.
11.17.10 Compare model fit with \(\chi ^{2}\Delta\), AIC, BIC
Warning in lavaan::lavTestLRT(uniDfit, corrF_fit, secondF, bifacF): lavaan WARNING:
Some restricted models fit better than less restricted models;
either these models are not nested, or the less restricted model
failed to reach a global optimum. Smallest difference =
-37.8284756558401Warning in lavaan::lavTestLRT(uniDfit, corrF_fit, secondF, bifacF): lavaan
WARNING: some models have the same degrees of freedom
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff
bifacF 43 6063.8 6189.3 262.62
corrF_fit 51 6010.0 6106.8 224.79 -37.828 0.00000 8
secondF 51 6010.0 6106.8 224.79 0.000 0.00000 0
uniDfit 54 6124.1 6210.2 344.97 120.178 0.38248 3
Pr(>Chisq)
bifacF
corrF_fit 1
secondF
uniDfit <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Warning in lavaan::lavTestLRT(secondF, bifacF): lavaan WARNING:
Some restricted models fit better than less restricted models;
either these models are not nested, or the less restricted model
failed to reach a global optimum. Smallest difference =
-37.8284756538201
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
bifacF 43 6063.8 6189.3 262.62
secondF 51 6010.0 6106.8 224.79 -37.828 0 8 111.17.11 Calculate omega hierarchical (\(\omega_{h}\)) and omega-hierarchical-subscales (\(\omega_{h-ss}\))
Given that our results favored the second-order structure, I will calculate model-based assessments of the omegas with that function (semTools::reliabilityL2) and object (secondF).
To use semTools we switch functions to reliabilityL2. The specification
omegaL1 omegaL2 partialOmegaL1
0.8832659 0.9237686 0.9336447 The estimate listed under omegaL1 (\(\omega_{ho}\)) represents the proportion of the course evaluation total score variance due to the higher-order factor. The value is 0.88 and, being above .80, indicates strong reliability.
We can apply the semTools::reliability() function to the second-order factor to obtain omega values for the subscales. Below the alpha coefficients, the omega values indicate how reliably each subscale measures its lower order factor. For example, 80% of the total variance of a total score comprised of only the 9 items in the AS scale is explained by the AS lower order factor.
TradPed Valued SCRPed
alpha 0.8973027 0.7573447 0.8037983
omega 0.9005696 0.8062411 0.8057420
omega2 0.9005696 0.8062411 0.8057420
omega3 0.9019489 0.8109489 0.7868658
avevar 0.6470672 0.6063643 0.5223301Subscale omegas range from .81 to .90.
In this case, \(\omega_{ho}\) (ho = higher order) (Flora, 2020b) represents the proportion of total-score variance that is due to the higher-order factor. As such, it represents the reliability of a total score for measuring a single construct that influences all items.
We obtained estimates of model-based internal consistency associated with the second-order model. Specifically, we calculated \(\omega_{ho}\), which represents the proportion of GRMSAAW total score variance due to the higher-order factor. The value of 0.88 indicates strong reliability. Similarly, we obtained omega values for the subscales. These ranged were 0.90, 0.81, and 0.81 for Traditional Pedagogy, Valued-by-the-Student, and Socially Responsive Pedagogy, respectively. Taken together, the omega values from our second order model suggest suggest a strong general factor and strong subscales.
11.17.12 APA style results with table(s) and figure
Because we have written mini-results throughout, we can assemble them into a full results section. Keep in mind that most CFA models will continue testing multidimensional models. Thus, the entire analysis continues in the next lesson and associated practice problem.
Model testing. To evaluate the models we, we used confirmatory factor analysis (CFA) in the R package, lavaan (v.0-6.17) with maximum likelihood estimation. Our sample size was 267 We selected fit criteria for their capacity to assess different aspects of the statistical analysis. As is common among SEM researchers, we reported the Chi-square goodness of fit (χ2). This evaluates the discrepancy between the unrestricted sample matrix and the restricted covariance matrix. Although the associated p-value indicates adequate fit when the value is non-significant, it is widely recognized that a large sample size can result in a statistically significant p value (Byrne, 2016b). The comparative fit index (CFI) is an incremental index, comparing the hypothesized model to the independent/baseline model. Adequate fit is determined when CFI values are at least .90 and perhaps higher than .95 (Kline, 2016). The root mean square error of approximation (RMSEA) takes into account the error of approximation in the population and expresses it per degree of freedom. As such, the fit indicator considers the complexity of the model. Ideal values are equal to or less than .05, values less than .08 represent reasonable fit, and values between .08 and .10 represent mediocre fit. The standardized root mean residual is a standardized measure of the mean absolute covariance residual – the overall difference between the observed and predicted correlations. Values greater than .10 may indicate poor fit and inspection of residuals is then advised. Kline (2016) advised researchers to be cautious when using these criteria as strict cut-offs. Elements such as sample size and model complexity should be considered when evaluating fit.
Our first model was unidimensional where each of the 12 items loaded onto a single factor representing overall course evaluations. The Chi-square index was statistically significant \((\chi^2(54)=344.97, p<.001)\) indicating likely misfit. The CFI value of .85 indicated poor fit. The RMSEA = .14 (90% CI [.13, .16]) suggested serious problems. The SRMR value of .07 was below the warning criteria of .10. The AIC and BIC values were 6124.13 and 6134.13, respectively, and will become useful in comparing subsequent models.
Our second model was a single-order, multidimensional model where each of the 12 items loaded onto one of four factors. Standardized pattern coefficients ranged between .74 and .85 on the TradPed factor, between .56 and .84 on the Valued factor, and between .57 and .85 on the SCRPed factor. The Chi-square index was statistically significant \((\chi^2(51) = 224.795, p < 0.001\) indicating some degree of misfit. The CFI value of .907 met the recommendation of .90 but fell below the recommendation of .95. The RMSEA = .113 (90% CI [.098, .128]) was higher than recommended. The SRMR value of .061 remained below the warning criteria of .10. The AIC and BIC values were 6009.95 and 6021.20, respectively.
Our third model represented a second order structure where three first-order factors loaded onto a second factor model. Across a variety of indices, model fit improved: \(\chi^{2}(51) = 224.80, p < .001, CFI = .907, RMSEA = .113, 90%CI(.098, .128), SRMR = .061\). Factor loadings ranged from .75 to .85 for the TradPed scale, .56 to .84 for the Valued-by-Me scale, .57 to .85 for the SCRPed scale, and .80 to .98 for the total scale.
The bifactor model regressed each item on its respective factor while simultaneously regressing each indicator onto an overall evaluation scale. The initial specification failed to converge. Adding the “std.lv = TRUE” to the lavaan::cfa function resulted in convergence. It also identified a negative covariance (i.e., a “Heywood” case). We resolved this issue by respecifying the model with a multiplication of the variance of the item (ClearPresentation) onto itself. This model had the second best fit of those compared thus far: \(\chi^2(43)=262.62, p < .001, CFI = .883, RMSEA = .138, 90%CI [.122, .155], SRMR = .084\) (the correlated factors and second order structures had the best fit). Factor loadings for the three factors ranged from .10 to .50 for the TradPed scale, .24 to .60 for the Valued-by-me scale, and .11 to .78 for the SCRPed scale. Factor loadings for the overall evaluation scale (g) ranged from .37 to .79.
As shown in our table of model comparisons, the Chi-square difference tests between models showed statistically significant differences between the unidimensional and correlated factors model (\(\chi ^{2}(3) = 120.178, p < .001\)). The second-order model and bifactor model did not differ from each other (\(\chi ^{2}(8) = -37.828, p = 1.000\)). The CFI, RMSEA, SRMR, AIC, and BIC values all favored the second-order and correlated factors models (which did not differ from each other).
We obtained estimates of model-based internal consistency associated with the second-order model. Specifically, we calculated \(\omega_{ho}\), which represents the proportion of GRMSAAW total score variance due to the higher-order factor. The value of 0.88 indicates strong reliability. Similarly, we obtained omega values for the subscales. These ranged were 0.90, 0.81, and 0.81 for Traditional Pedagogy, Valued-by-the-Student, and Socially Responsive Pedagogy, respectively. Taken together, the omega values from our second order model suggest a strong general factor and strong subscales.
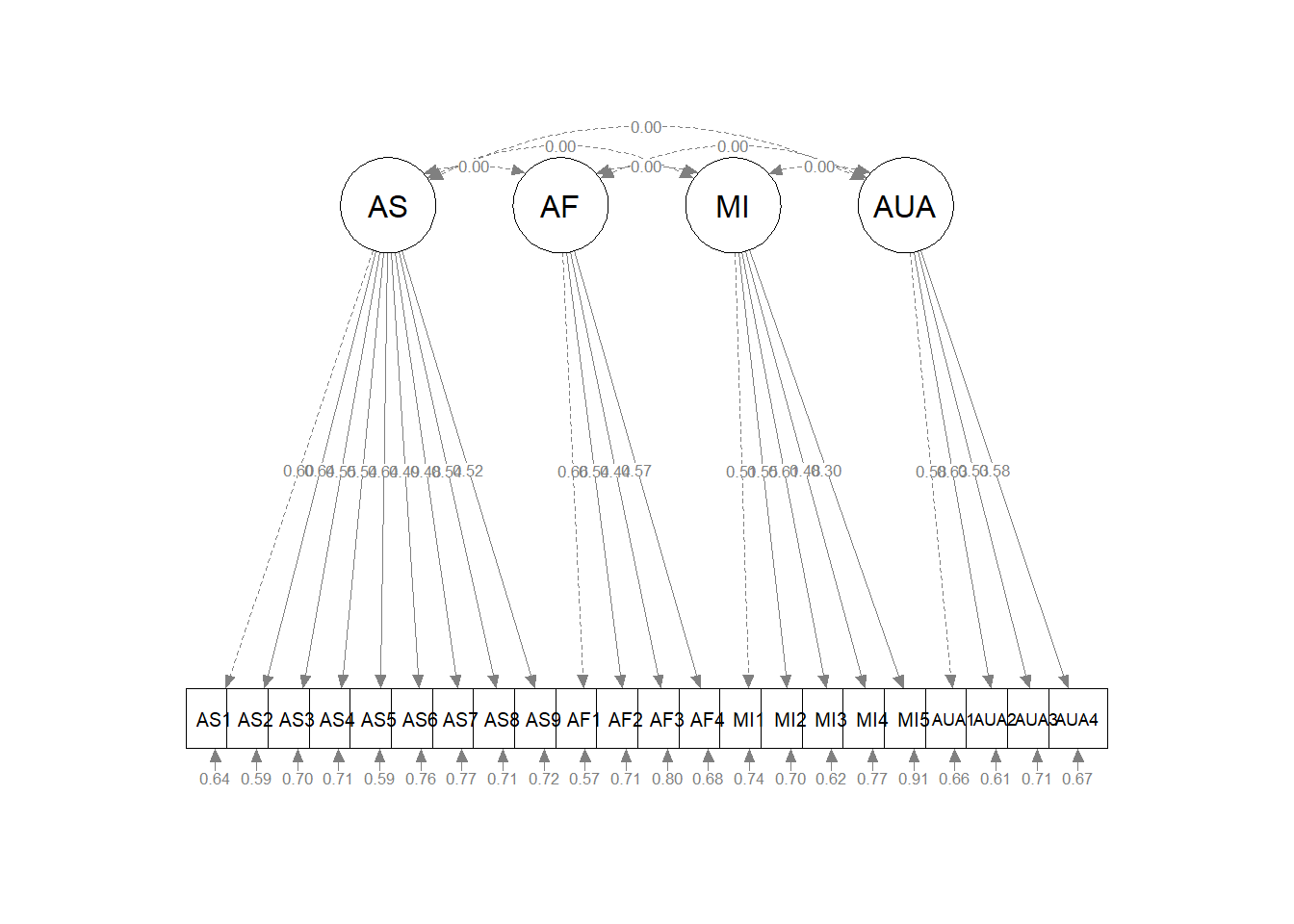
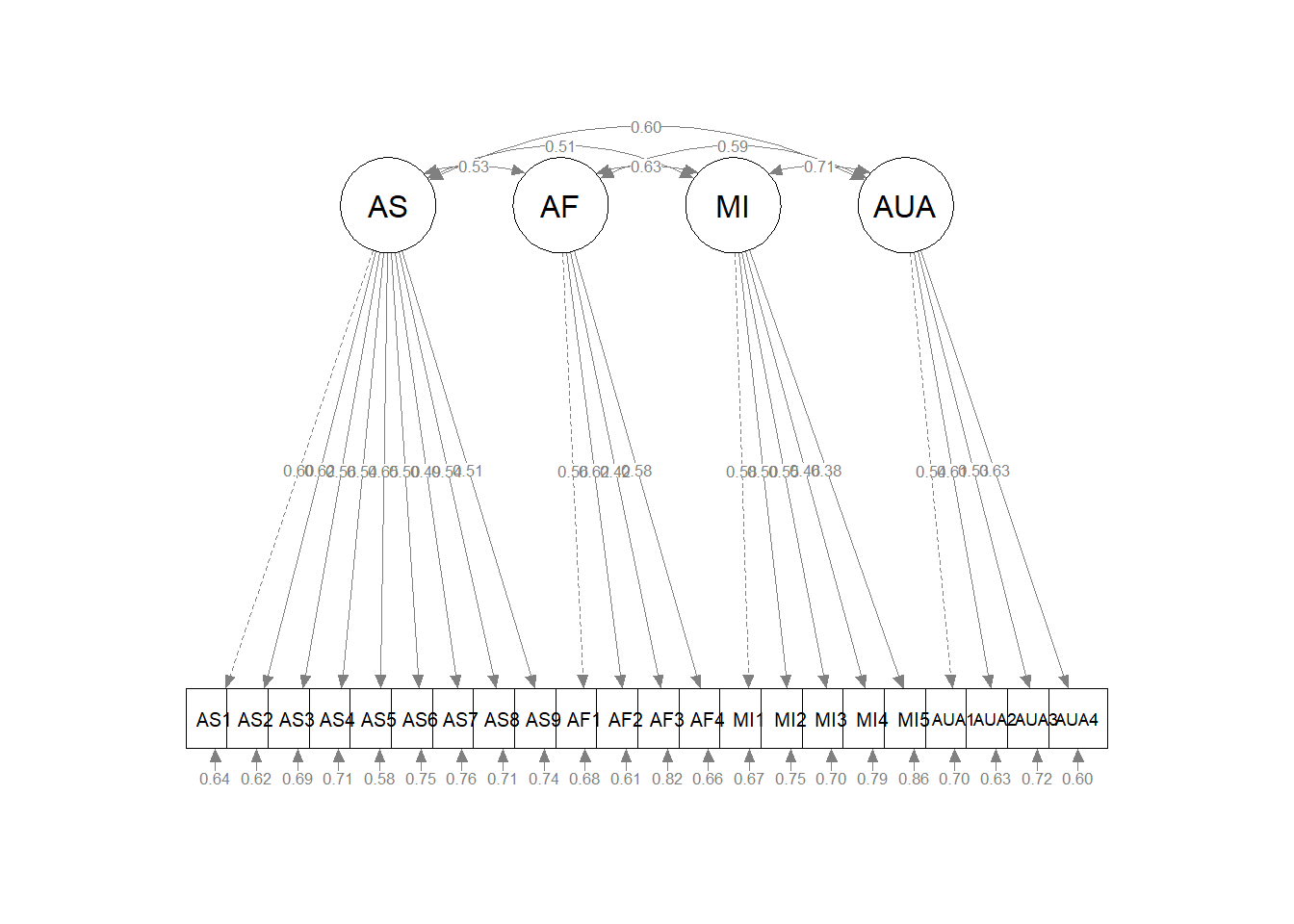
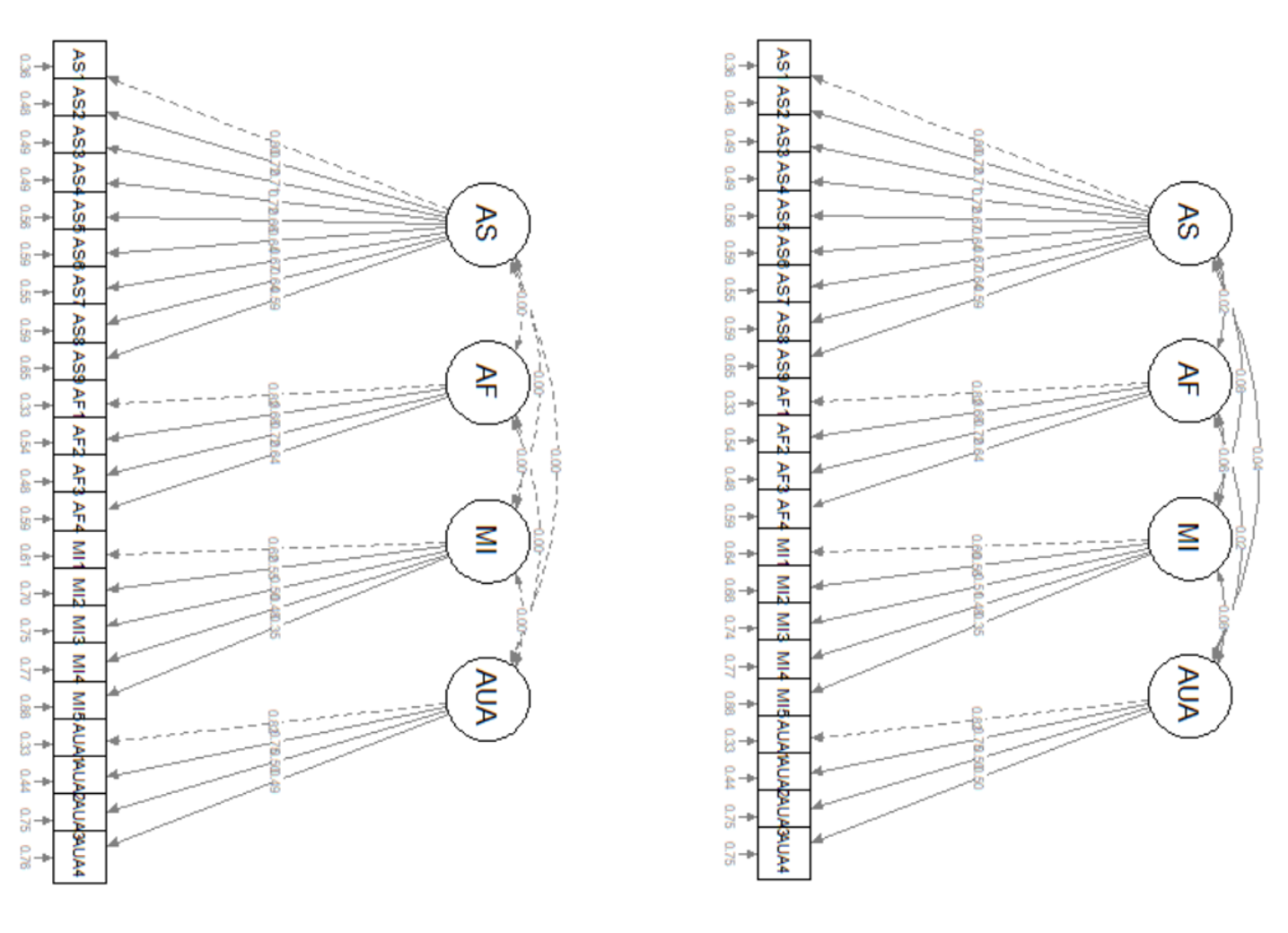
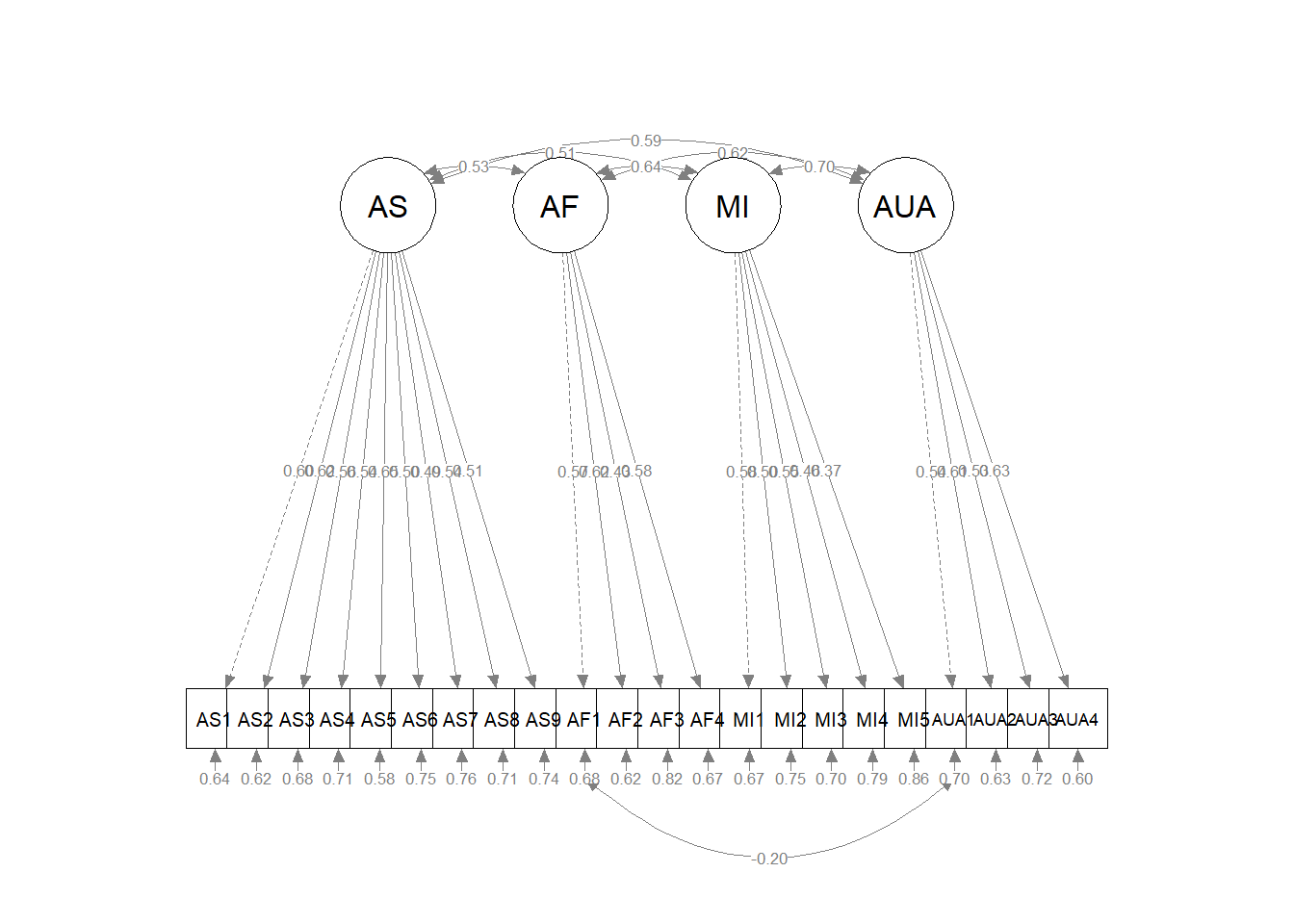
 Source:
Source: